福建省福州市闽侯县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-29 类型:期中考试
一、单选题
-
1. 五边形的内角和为( )A、720° B、540° C、360° D、180°2. 下列运算正确的是( )A、 B、 C、 D、3. 对多项式 进行添括号,正确的是( )A、 B、 C、 D、4. 在下列长度的四根木棒中,能与 , 长的两根木棒钉成一个三角形的是( )A、 B、 C、 D、5. 在平面直角坐标系中,点 关于y轴对称的点的坐标是( )A、 B、 C、 D、6. 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
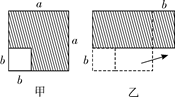 A、(a+b)2=a2+2ab+b2 B、(a-b)2=a2-2ab+b2 C、a2-b2=(a+b)(a-b) D、(a+2b)(a-b)=a2+ab-2b27. 从八边形一个顶点出发可以引( )条对角线.A、4 B、5 C、8 D、208. 如图, , , , ,则 的度数为( )
A、(a+b)2=a2+2ab+b2 B、(a-b)2=a2-2ab+b2 C、a2-b2=(a+b)(a-b) D、(a+2b)(a-b)=a2+ab-2b27. 从八边形一个顶点出发可以引( )条对角线.A、4 B、5 C、8 D、208. 如图, , , , ,则 的度数为( ) A、40° B、32° C、36° D、30°9. 如图所示的正方形网格中,网格线的交点称为格点,已知点A,B是两格点,如果C也是图中的格点,若 是等腰三角形,则满足条件的点C的个数是( )
A、40° B、32° C、36° D、30°9. 如图所示的正方形网格中,网格线的交点称为格点,已知点A,B是两格点,如果C也是图中的格点,若 是等腰三角形,则满足条件的点C的个数是( ) A、4 B、6 C、8 D、1010. 在平面直角坐标系 中,点 , , , ,若 平分 ,且 ,则a的值为( )A、2 B、3 C、5 D、3或5
A、4 B、6 C、8 D、1010. 在平面直角坐标系 中,点 , , , ,若 平分 ,且 ,则a的值为( )A、2 B、3 C、5 D、3或5二、填空题
-
11. 如图,木工师傅做门框时,常用木条 固定长方形门框 ,使其不变形,这种做法的依据是.
 12. 计算 .13. 已知在平面直角坐标系中,点 , , ,若点A、B、C能构成三角形,则m应满足的条件是.14. 已知 ,点 在 的内部, 与 关于 对称, 与 关于 对称, .15. 如图,在 中, , , , ,则 的度数等于.
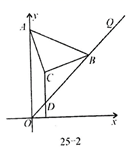
12. 计算 .13. 已知在平面直角坐标系中,点 , , ,若点A、B、C能构成三角形,则m应满足的条件是.14. 已知 ,点 在 的内部, 与 关于 对称, 与 关于 对称, .15. 如图,在 中, , , , ,则 的度数等于.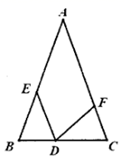 16. 如图,过点 的直线 轴, ,点B在x轴的正半轴上, 平分 交l于点C,则点C的坐标是.
16. 如图,过点 的直线 轴, ,点B在x轴的正半轴上, 平分 交l于点C,则点C的坐标是.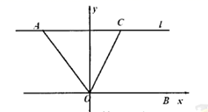 17. 如图,已知点B,E,C,F在同一直线上, , ,________,求证: .
17. 如图,已知点B,E,C,F在同一直线上, , ,________,求证: . (1)、请添加一个条件(只需写出一个),使命题成立;(2)、请根据(1)中添加的条件,完成证明.
(1)、请添加一个条件(只需写出一个),使命题成立;(2)、请根据(1)中添加的条件,完成证明.三、解答题
-
18. 计算(1)、(2)、19. 如图,已知 中, , , 是边 上的高,求 的度数.
 20. 如图,网格图中的每小格均是边长是1的正方形, 与 的顶点均在格点上,请完成下列各题:
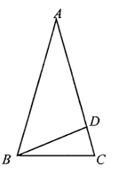
20. 如图,网格图中的每小格均是边长是1的正方形, 与 的顶点均在格点上,请完成下列各题: (1)、在平面直角坐标系中画出与 关于x轴对称的 ,并写出将 沿着x轴向右平移几个单位后得到 ;(2)、在x轴上求作一点P,使得 的值最大。(要求:保留画图痕迹并直接写出点P的坐标.)21. 如图是屋架设计图的一部分,点D是斜梁 中点,立柱 , 垂直于横梁 , , 。立柱 , 要多长?
(1)、在平面直角坐标系中画出与 关于x轴对称的 ,并写出将 沿着x轴向右平移几个单位后得到 ;(2)、在x轴上求作一点P,使得 的值最大。(要求:保留画图痕迹并直接写出点P的坐标.)21. 如图是屋架设计图的一部分,点D是斜梁 中点,立柱 , 垂直于横梁 , , 。立柱 , 要多长? 22. 求证:全等三角形的对应角平分线相等.(提示:本题须根据命题的题设与结论,画图,写出已知、求证,并证明.)
22. 求证:全等三角形的对应角平分线相等.(提示:本题须根据命题的题设与结论,画图,写出已知、求证,并证明.)