山东省潍坊市青州市2019-2020学年七年级上学期数学期中试卷

试卷更新日期：2020-09-28 类型：期中考试

进入出卷网下载

一、单选题

1. 如果 $- 4 m$ 表示向西运动4米，那么向东运动2米应记作（）

A、 $+ 2 m$ B、 $- 2 m$ C、 $+ 4 m$ D、 $- 4 m$

查看试题解析
2. 将如图所示的平面困形烧虚线旋转一周所得的立体图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列调查方式合适的是（　　）

A、为了了解人们保护水资源的意识，采用抽样调查的方式 B、为了了解中央电视台春节联欢晚会的收视率，采取普查方式 C、对嫦娥三号卫星零部件的检查，采用抽样调查的方式 D、为了了解一批手机的使用寿命，采用普查方式

查看试题解析
4. 下列说法正确的是（）

A、画射线 $O A = 5 c m$ B、三条直线相交有3个交点 C、若点C在线段AB外，则 $A C < A B$ D、反向延长射线OA（0为端点）

查看试题解析
5. 下列各组数中，数值相等的是（）

A、 $- 2^{2}$ 和 ${(- 3)}^{2}$ B、 ${(- 5)}^{3}$ 和 $- 5^{3}$ C、 ${(- 3)}^{2}$ 和 $- 3^{2}$ D、 $\frac{3^{2}}{5}$ 和 ${(\frac{3}{5})}^{2}$

查看试题解析
6. 在 $- (- 2), - | - 7 |, - 1^{2019} \times 0, - {(- 1)}^{3}, - (+ \frac{5}{2}), - 2^{4}$ 中，非正数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. “十三五”以来，我国启动实施了农村饮水安全巩固提升工程．截止去年9月底，各地已累计完成投资 $1.002 \times 10^{11}$ 元．数据 $1.002 \times 10^{11}$ 可以表示为（）

A、10.02亿 B、100.2亿 C、1002亿 D、10020亿

查看试题解析
8. 在数轴上表示有理数a，b，c的点如图所示，若 $a c < 0 ， b + c < 0$ .则下列式子一定成立的是（）

A、 $a + c > 0$ B、 $a b c < 0$ C、 $| b | < | c |$ D、 $| b | > | c |$

查看试题解析
9. 已知 $| m | = 5, | n - 3 | = - {(p - 2)}^{2}$ ，则 $\frac{m n}{p}$ 的值为（）

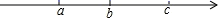A、 $- \frac{15}{2}$ B、 $\frac{15}{2}$ C、 $- \frac{15}{2}$ 或 $\frac{15}{2}$ D、-4或4

查看试题解析
10. 下面的平面展开图与图下方的立体图形名称不相符的是（）

A、 B、 C、 D、

查看试题解析
11. 一张纸的厚度大约为0.07mm.如果将这张纸连续对折15次，这时它的厚度最接近于（）

A、三层楼的高度 B、篮球运动员姚明的身高 C、数学课本的厚度 D、书桌的高度

查看试题解析
12. 如图是我市某公司2019年2-4月份资金投放总额与利润总额统计示意图，根据图中的信息判断：①利润最高的是4月份；②合计三个月的利润率为36.4%；③4月份的利润率比2月份的利润率高4.4%（说明：利润率=利润总额÷投资总额×100%）其中正确的是（）

A、①②③ B、①② C、①③ D、②③

查看试题解析

二、填空题

13. 用“>”，“<”或“=” $- \frac{7}{8}$ $- \frac{8}{9}$

查看试题解析
14. “曙光4000A超级服务器”的峰值计算速度达到每秒8061000000000将这个数四舍五入得到近似数 $8.1 \times 10^{12}$ ，则这个近似数是精确到位.

查看试题解析
15. 如图是某中学七年级学生视力统计图，其中近视400度以上的学生所在扇形的圆心角为度.

查看试题解析
16. 下列有四个生活、生产现象：①植树时，只要定出两棵树的位置，就能确定同一行所在的直线；②有两个钉子就可以把木条固定在墙上；③把弯曲的公路改直，就能缩短路程，④从A地到B地架设电线，总是尽可能沿着线段AB架设：其中可用基本事实“两点之间，线段最短”来解释的现象有(填写正确说法的序号）

查看试题解析
17. 如图所示，若图中共有m条线段，n条射线，则 $m + n =$ .

查看试题解析
18. 如下表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第2019个格子中的数为.

查看试题解析

三、解答题

19. 计算下列各题：

(1)、 $18 + (- 12) + (- 21) - (- 12)$

(2)、 $- \frac{23}{4} + (+ \frac{17}{7}) + (- \frac{5}{4}) - (- \frac{4}{7})$

(3)、 $\frac{27}{4} \times (\frac{1}{3} - 1) \div {(- 3)}^{2}$

(4)、 $- 13 \times \frac{2}{3} - 0.34 \times \frac{2}{7} + \frac{1}{3} \times (- 13) - \frac{5}{7} \times 0.34$

(5)、 $- 1^{4} - (1 - 0.5) \times \frac{1}{3} \times [1 - {(- 2)}^{2}]$

查看试题解析
20. 按要求解题：

(1)、A，B，M，N四点如图所示，读下列语句，按要求作出图形（不写作法）
①连接AB；

②在线段AB的延长线上取点C，使 $B C = 2 A B$ ；

③连接AN，BM，它们相交于点P；

(2)、在（1）题图中，若 $A B = 2 c m$ .D为AB的中点，E为AC的中点，求DE的长.

查看试题解析
21. 某校组织七年级学生体育健康抽测，（1）班25名学生的成绩（满分为100分）统计如下：
90，74，88，65，98，76，81，42，85，70，55，80，95，88，72，87，61，56，76，66，78，72，82，63，100.

(1)、90分及以上为A级，75-89分为B级，60-74分为C级，60分以下为D级，请把下面表格补充完整，并将图中的条形图补充完整；

等级

A

B

C

D

人数

8

(2)、该校七年级共有1000名学生，如果60分以上为合格，请估计七年级有多少人合格？

(3)、请选择合适的统计图表示出抽测中每一个等级的人数占总人数的百分比.

查看试题解析
22. 已知：a，b互为相反数，c，d互为倒数，x的绝对值是2.
求 $x^{2} - (a + b + c d) x + {(a + b)}^{2019} + {(- c d)}^{2020}$ 的值.

查看试题解析
23. 定义：如果 $2^{b} = n$ ，那么称b为n的布谷数，记为 $b = g (n)$ .
例如：因为 $2^{3} = 8$ ，所以 $g (8) = g (2^{3}) = 3$ ，

因为 $2^{10} = 1024$ ，

所以 $g (1024) = g (2^{10}) = 10$ .

(1)、根据布谷数的定义填空：g（2）= ， g（32）=.

(2)、布谷数有如下运算性质：
若m，n为正整数，则 $g (m n) = g (m) + g (n)$ ， $g (\frac{m}{n}) = g (m) - g (n)$ .

根据运算性质解答下列各题：

①已知 $g (7) = 2.807$ ，求 $g (14)$ 和 $g (\frac{7}{4})$ 的值；

②已知 $g (3) = p$ .求 $g (18)$ 和 $g (\frac{3}{16})$ 的值.

查看试题解析
24. 已知a是最大的负整数， $b = - | - 5 |$ ，c是-4的相反数，且a，b，c分别是点A．B．C在数轴上对应的数.

(1)、求a，b，c的值，并在数轴上标出点A，B，C；

(2)、在数轴上，若D到A的距离刚好是3，则D点叫做A的“幸福点”.则A的幸福点D所表示的数应该是.

(3)、若动点P从点B出发沿数轴向正方向运动，动点Q同时从点A出发也沿数轴向正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒1个单位长度，求运动几秒后，点P可以追上点Q?

(4)、在数轴上，若M到A，C的距离之和为6，则M叫做A，C的“幸福中心”.请直接写出所有点M在数轴上对应的数.

查看试题解析

等级	A	B	C	D
人数			8