山东省威海市文登区八校2019-2020学年七年级上学期数学期中试卷
试卷更新日期:2020-09-28 类型:期中考试
一、单选题
-
1. 下列图形中,轴对称图形的个数为( )
 A、1个 B、2个 C、3个 D、4个2. 根据下列已知条件,能画出唯一的△ABC的是( )A、AB=3,BC=4,∠C=40° B、AB=4,BC=3,∠A=30° C、∠C=90°,AB=6 D、∠A=60°,∠B=45°,AB=43. 现有两根木棒,它们的长分别是20 和30 ,若不改变木棒的长短,要钉成一个三角形木架,则应在下列四根木棒中选取( )A、9 的木棒 B、36 的木棒 C、50 的木棒 D、60 的木棒4. 如图,△ABC的顶点A、B、C都在小正方形的顶点上,在格点F、G、H、I中选出一个点与点D、点E构成的三角形与△ABC全等,则符合条件的点共有( )
A、1个 B、2个 C、3个 D、4个2. 根据下列已知条件,能画出唯一的△ABC的是( )A、AB=3,BC=4,∠C=40° B、AB=4,BC=3,∠A=30° C、∠C=90°,AB=6 D、∠A=60°,∠B=45°,AB=43. 现有两根木棒,它们的长分别是20 和30 ,若不改变木棒的长短,要钉成一个三角形木架,则应在下列四根木棒中选取( )A、9 的木棒 B、36 的木棒 C、50 的木棒 D、60 的木棒4. 如图,△ABC的顶点A、B、C都在小正方形的顶点上,在格点F、G、H、I中选出一个点与点D、点E构成的三角形与△ABC全等,则符合条件的点共有( ) A、1个 B、2个 C、3个 D、4个5. 在3×3的正方形网格中,将三个小正方形涂色如图所示,若移动其中一个涂色小正方形到空白方格中,与其余两个涂色小正方形重新组合,使得新构成的整个图案是一个轴对称图形,则这样的移法共有( )
A、1个 B、2个 C、3个 D、4个5. 在3×3的正方形网格中,将三个小正方形涂色如图所示,若移动其中一个涂色小正方形到空白方格中,与其余两个涂色小正方形重新组合,使得新构成的整个图案是一个轴对称图形,则这样的移法共有( ) A、5种 B、7种 C、9种 D、10种6. 如图,△ABC的面积为1cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )cm2
A、5种 B、7种 C、9种 D、10种6. 如图,△ABC的面积为1cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )cm2 A、 B、 C、 D、7. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中 , , , ,则 ( )
A、 B、 C、 D、7. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中 , , , ,则 ( ) A、25 B、36 C、32 D、408. 长为8,5,4,3的四根木条,选其中三根组成三角形,选法有( )
A、25 B、36 C、32 D、408. 长为8,5,4,3的四根木条,选其中三根组成三角形,选法有( )
A、1种 B、2种 C、3种 D、4种9. 将根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,设筷子露在杯子外面的长度hcm,则h的取值范围是( ) A、 B、 C、 D、10. 已知:如图, 内一点 , , 分别P是关于 、 的对称点, 交 于M,交 于N,若 ,则 的周长是( )
A、 B、 C、 D、10. 已知:如图, 内一点 , , 分别P是关于 、 的对称点, 交 于M,交 于N,若 ,则 的周长是( ) A、 B、 C、 D、11. 如上图,透明的圆柱形容器(容器厚度忽略不计)的高为12 ,底面周长为10 ,在容器内壁离容器底部3 的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
A、 B、 C、 D、11. 如上图,透明的圆柱形容器(容器厚度忽略不计)的高为12 ,底面周长为10 ,在容器内壁离容器底部3 的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( ) A、13 B、12 C、15 D、1612. 如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )
A、13 B、12 C、15 D、1612. 如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( ) A、140° B、100° C、50° D、40°
A、140° B、100° C、50° D、40°二、填空题
-
13. 已知 中, ,则这个三角形是三角形.14.
如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片即可
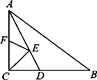
 15. 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D , 若AC=8,BC=6,则CD= .
15. 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D , 若AC=8,BC=6,则CD= . 16. 如图,在△ABC中,∠A=80°,∠ABC和∠ACD的平分线交于点E , 则∠E= .
16. 如图,在△ABC中,∠A=80°,∠ABC和∠ACD的平分线交于点E , 则∠E= .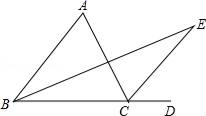 17. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD , 则∠A′DB的度数为 .
17. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD , 则∠A′DB的度数为 . 18. 如下图,点 是 外的一点,点M,N分别是 两边上的点,点P关于 的对称点Q恰好落在线段 上,点P关于 的对称点R落在 的延长线上.若 , , ,则线段 的长为 .
18. 如下图,点 是 外的一点,点M,N分别是 两边上的点,点P关于 的对称点Q恰好落在线段 上,点P关于 的对称点R落在 的延长线上.若 , , ,则线段 的长为 .
三、解答题
-
19. 尺规作图(只保留作图痕迹,不要求写出作法)
如图,已知 和线段a、b
求作:
⑴ ,使 , , .
⑵在(1)的条件下,作 边上的中线 .
 20. 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
20. 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.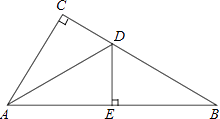 (1)、求证:△ACD≌△AED;(2)、若∠B=30°,CD=1,求BD的长.21. A,B两个居民楼在公路同侧,它们离公路的距离分别为AE=200米,BF=70米,它们的水平距离EF=390米.现欲在公路旁建一个超市P,使超市到两居民楼的距离相等,则超市应建何处?为什么?
(1)、求证:△ACD≌△AED;(2)、若∠B=30°,CD=1,求BD的长.21. A,B两个居民楼在公路同侧,它们离公路的距离分别为AE=200米,BF=70米,它们的水平距离EF=390米.现欲在公路旁建一个超市P,使超市到两居民楼的距离相等,则超市应建何处?为什么? 22. 已知, , , 于E, 于D.
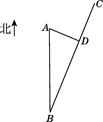
22. 已知, , , 于E, 于D. (1)、如图1,求证: ≌ ;(2)、若点D在 的内部(如图2), , ,求 的长.23. 如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?
(1)、如图1,求证: ≌ ;(2)、若点D在 的内部(如图2), , ,求 的长.23. 如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?