山东省泰安市2019-2020学年七年级上学期数学期中试卷
试卷更新日期:2020-09-28 类型:期中考试
一、单选题
-
1. 如下图,线段 是 的高的是( )A、
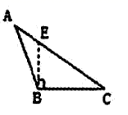 B、
B、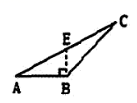 C、
C、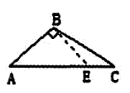 D、
D、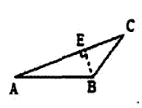 2. 如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列中的( )
2. 如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列中的( ) A、AB=CD B、EC=BF C、∠A=∠D D、AB=BC3. 在下列长度的三条线段.不能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列图形中,是轴对称图形的是( )A、
A、AB=CD B、EC=BF C、∠A=∠D D、AB=BC3. 在下列长度的三条线段.不能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列图形中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,已知 ,那么添加下列一个条件后,仍无法判定 ≌ 的是( )
5. 如图,已知 ,那么添加下列一个条件后,仍无法判定 ≌ 的是( )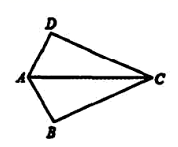 A、 B、 C、 D、6. 如图, .D点在 上,将D点分别以 、 为对称轴,画出对称点E、F,并连接 、 ,根据图中标示的角度,则 的度数是( )
A、 B、 C、 D、6. 如图, .D点在 上,将D点分别以 、 为对称轴,画出对称点E、F,并连接 、 ,根据图中标示的角度,则 的度数是( ) A、143 B、134 C、129 D、1247. 若等腰三角形的周长为10 ,其中一边长为4 ,则该等腰三角形的底边长为( )A、4 B、6 C、4 或2 D、4 或68. 已知一直角三角形的木板,三边的平方和为1800 ,则斜边长为( )A、45 B、30 C、60 D、1209. 如图,在 . , , , 平分 ,则点D到 的距离等于( )
A、143 B、134 C、129 D、1247. 若等腰三角形的周长为10 ,其中一边长为4 ,则该等腰三角形的底边长为( )A、4 B、6 C、4 或2 D、4 或68. 已知一直角三角形的木板,三边的平方和为1800 ,则斜边长为( )A、45 B、30 C、60 D、1209. 如图,在 . , , , 平分 ,则点D到 的距离等于( ) A、6 B、5 C、3 D、210. 下列说法正确的是( )A、周长相等的两个三角形全等 B、有两边和其中一边的对角对应相等的两个三角形全等 C、三角分别相等的两个三角形全等 D、有两角和其中一角的对边对应相等的两个三角形全等.11. 三角形的三边长分别为6,8,10,那么最长边上的高为( )A、4.8 B、5 C、6 D、812. 如图,在 . ,分别以点B和点C为圆心,大于 的长为半径作弧,两弧相交于D、E两点,作直线 交 于点F,交 于点G,连接 , , ,则 的长为( )
A、6 B、5 C、3 D、210. 下列说法正确的是( )A、周长相等的两个三角形全等 B、有两边和其中一边的对角对应相等的两个三角形全等 C、三角分别相等的两个三角形全等 D、有两角和其中一角的对边对应相等的两个三角形全等.11. 三角形的三边长分别为6,8,10,那么最长边上的高为( )A、4.8 B、5 C、6 D、812. 如图,在 . ,分别以点B和点C为圆心,大于 的长为半径作弧,两弧相交于D、E两点,作直线 交 于点F,交 于点G,连接 , , ,则 的长为( ) A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7二、填空题
-
13. 等腰三角形的一个内角为40°,则顶角的度数为 .14. 一个三角形的三边为2、5、x , 另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= .15. 如图,点D在 的延长线上, 于点E,交 于点F,若 , ,则 的度数为 .
 16. 若三角形的三边满足a:b:c=5:12:13,则这个三角形中最大的角为度.17. 在 . : : 1:2:3, 于点D,若 ,则18. 如图,已知AB∥CD,AD∥BC,E.F是BD上两点,且BF=DE,则图中共有对全等三角形.
16. 若三角形的三边满足a:b:c=5:12:13,则这个三角形中最大的角为度.17. 在 . : : 1:2:3, 于点D,若 ,则18. 如图,已知AB∥CD,AD∥BC,E.F是BD上两点,且BF=DE,则图中共有对全等三角形. 19. “赵爽弦图”巧妙的利用面积关系证明了勾股定理,是我国古代数学的骄傲,如下图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为a,较短的直角边长为b,若 ,大正方形的面积为 ,则小正方形的面积为 .
19. “赵爽弦图”巧妙的利用面积关系证明了勾股定理,是我国古代数学的骄傲,如下图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为a,较短的直角边长为b,若 ,大正方形的面积为 ,则小正方形的面积为 . 20. 如图,
20. 如图,
在 和 . , , , ,连接 , 交于点M,连接 ,下列结论:① ;② ;③ 平分 ;④ 平分 ,其中正确的序号是 .
三、解答题
-
21. 如图, ∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,为什么.
 22. 如图,在等腰三角形 . ,点D为 边上的中点, 于点E, 于点F,则 与 相等吗?请说明理由.
22. 如图,在等腰三角形 . ,点D为 边上的中点, 于点E, 于点F,则 与 相等吗?请说明理由. 23. 如图,某住宅小区在施工过程中留下了一块空地(图中的四边形 ),经测量,在四边形 . , , , , .
23. 如图,某住宅小区在施工过程中留下了一块空地(图中的四边形 ),经测量,在四边形 . , , , , . (1)、若连接 ,则 是直角三角形吗?为什么?(2)、小区为美化环境,欲在空地上铺草坪,已知草坪每平方米150元,试问铺满这块空地共需花费多少元?24. 已知:在 . ,求作:以 边为一边的等腰三角形,使它的第三个顶点在 的其他边上,请在下面的三个图形中用尺规作图法作出不同的等腰三角形,保留作图痕迹.
(1)、若连接 ,则 是直角三角形吗?为什么?(2)、小区为美化环境,欲在空地上铺草坪,已知草坪每平方米150元,试问铺满这块空地共需花费多少元?24. 已知:在 . ,求作:以 边为一边的等腰三角形,使它的第三个顶点在 的其他边上,请在下面的三个图形中用尺规作图法作出不同的等腰三角形,保留作图痕迹.


