山东省济南市市中区2019-2020学年七年级上学期数学期中试卷

试卷更新日期：2020-09-28 类型：期中考试

进入出卷网下载

一、单选题

1. ﹣3的相反数是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、 $- 3$ D、 $3$

查看试题解析
2. 国家主席习近平提出“金山银山，不如绿水青山”，国家环保部大力治理环境污染，空气质量明显好转，将惠及13.75亿中国人，这个数字用科学记数法表示为（）

A、13.75×10⁶ B、13.75×10⁵ C、1.375×10⁸ D、1.375×10⁹

查看试题解析
3. 如图，四个几何体分别为长方体、圆柱体、球体和三棱桂，这四个几何体中截面不可能是长方形的几何体是（　　）

A、 B、 C、 D、

查看试题解析
4. 单项式 $- 3 x y^{2} z^{3}$ 的系数和次数分别是（）

A、 $- 1$ ，6 B、6， $- 1$ C、6， $- 3$ D、 $- 3$ ，6

查看试题解析
5. 下列运算，结果正确的是（）

A、2ab－2ba=0 B、2a²+3a²=6a² C、3xy－4xy=－1 D、2x³+3x³=5x⁶

查看试题解析
6. 下列各组式子中，为同类项的是（）

A、5 $x^{2}$ y与－2x $y^{2}$ B、4x与4 $x^{2}$ C、－3xy与 $\frac{3}{2}$ yx D、6 $x^{3}$ $y^{4}$ 与－6 $x^{3} z^{4}$

查看试题解析
7. 已知代数式x+2y+1的值是3，则代数式2x+4y+1的值是（）

A、4 B、5 C、7 D、不能确定

查看试题解析
8. 如图是一数值转换机，若输入的数为 $- \frac{1}{2}$ ，则输出的结果为（）

A、 $- 3$ B、 $- 6$ C、0 D、3

查看试题解析
9. 有理数a，b在数轴上的位置如图所示，则下列各式：
①a+b＞0；②a﹣b＞0；③|b|＞a；④ab＜0．一定成立的是（）

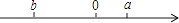A、①②③ B、③④ C、②③④ D、①③④

查看试题解析
10. ${(M - 6)}^{2} + | N - 8 | = 0$ ，则 $M - N$ 的值是（）

A、0 B、 $- 2$ C、6 D、1

查看试题解析
11. 用火柴棒按下面的方式搭图形，搭第1个图形需要7根火柴棒，搭第2个图形需要12根火柴棒，搭第3个图形需要17根火柴棒搭，……，照这样的规律搭下去，第 $n$ 个图形需要的火柴棒的根数是（）

A、 $5 n - 2$ B、 $5 n + 1$ C、 $5 n + 2$ D、 $5 n + 3$

查看试题解析
12. 图①是正方体的平面展开图，六个面的点数分别为1点、2点、3点、4点、5点、6点，将点数朝外折叠成一枚正方体骰子，并放置于水平桌面上，如图②所示，若骰子初始位置为图②所示的状态，将骰子向右翻滚 $90 °$ ，则完成1次翻转，此时骰子朝下一面的点数是2，那么按上述规则连线完成2次翻折后，骰子朝下一面的点数是3点；连续完成2019次翻折后，骰子朝下一面的点数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 比较大小： $- 5.1$ $- 6.1$ ．

查看试题解析
14. 已知甲地的海拔高度是300m，乙地的海拔高度是－50m，那么甲地比乙地高m.

查看试题解析
15. 一个棱柱有9个面，那么它有棱．

查看试题解析
16. 在数轴上与﹣1相距3个单位长度的点表示的有理数是．

查看试题解析
17. 已知m、n是系数，且 $m x^{2} - 2 x y + y$ 与 $3 x^{2} + 2 n x y + 3 y$ 的差中不含二次项，则 $m + 3 n =$ ．

查看试题解析
18. a、b为有理数，现在规定了一种新的运算“ $\oplus$ ”： $a \oplus b = a^{2} - a b + a - 1$ ，如： $2 \oplus (- 5) = 2^{2} - 2 \times (- 5) + 2 - 1 = 15$ ，则 $(2 \oplus 3) \oplus (- 3) =$ ．

查看试题解析

三、解答题

19. 画出如图所示几何体的三视图．

查看试题解析
20. 画一条数轴，把下列各数表示在数轴上，并用“ $<$ ”连接：
3， $- 2.5$ ， $- 3$ ，0.5， $4 \frac{1}{2}$ ．

查看试题解析
21. 计算：

(1)、 $(- 14) - (+ 6) - (- 31) + (- 19)$ ．

(2)、 $- 3^{2} + {(- \frac{2}{3})}^{2} \times 9 - {(- 1)}^{3}$

(3)、 $(- 36) \times (\frac{5}{4} - \frac{5}{6} - \frac{11}{12})$

查看试题解析
22. 化简：

(1)、－3m＋2m－5m；

(2)、(2a²－1＋2a)－(a－1＋a²)．

查看试题解析
23. 回答下列各题．

(1)、先化简，再求值： $2 (3 a^{2} b - a b^{2}) - (a b^{2} + 2 a^{2} b)$ ，其中 $a = - 2$ ， $b = 1$ ．

(2)、小黄做一道题：“已知两个多项式A，B，计算 $A - B$ ”，小黄误将 $A - B$ 看成 $A + B$ ，求得结果是 $9 x^{2} - 2 x + 7$ ，若 $B = x^{2} + 3 x - 2$ ，请你帮助小黄求出 $A - B$ 的符合题意答案．

查看试题解析

24. 某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入，下表是某周的生产情况（超产记为正、减产记为负）：

星期	一	二	三	四	五	六	七
增减产值	$+ 5$	$- 2$	$- 4$	$+ 13$	$- 10$	$+ 16$	$- 9$

(1)、根据记录的数据可知该厂星期五生产自行车辆．

(2)、根据记录的数据可知该厂本周实际生产自行车辆．

(3)、该厂实行每日计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元，若没有完成任务，少生产一辆扣20元，那么该厂工人这一周的工作总额是多少元？

查看试题解析

25. 一位画家有若干个边长为1cm的正方体，他在地面上把它们摆成如图（三层）的形式，然后，他把露出的表面都涂上颜色．

(1)、图中的正方体一共有多少个？

(2)、一点颜色都没涂上颜色的正方体有多少个？

(3)、如果画家按此方式摆成七层，那又要多少个正方体？同样涂上颜色，又有多少个正方体没有涂上一点颜色？

查看试题解析
26. 观察下列式子：
$1 \times 3 + 1 = 4 = 2^{2}$ ；

$2 \times 4 + 1 = 3^{2}$ ；

$3 \times 5 + 1 = 4^{2}$ ；

$4 \times 6 + 1 = 5^{2}$ ；

……

(1)、请你找出规律并计算： $7 \times 9 + 1 =$ $^{2}$ ．

(2)、用含n的式子表示上面的规律：．

(3)、用找到的规律计算： $(1 + \frac{1}{1 \times 3}) (1 + \frac{1}{2 \times 4}) (1 + \frac{1}{3 \times 5}) (1 + \frac{1}{4 \times 6}) \dots (1 + \frac{1}{2011 \times 2013})$ ．

查看试题解析
27. 已知a是最大的负整数，b、c满足 $（ b-3 ）^{2} + | c + 4 | = 0$ ，且a，b，c分别是点A，B，C在数轴上对应的数.

(1)、求a，b，c的值，并在数轴上标出点A，B，C；

(2)、若动点P从C出发沿数轴正方向运动，点P的速度是每秒2个单位长度，运动几秒后，点P到达B点?

(3)、在数轴上找一点M，使点M到A，B，C三点的距离之和等于13，请直接写出所有点M对应的数.(不必说明理由)

查看试题解析