山东省东营市广饶县2019-2020学年七年级上学期数学期中试卷

试卷更新日期：2020-09-28 类型：期中考试

进入出卷网下载

一、单选题

1. 下列是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列条件中，不能断定△ABC为直角三角形的是（）

A、 $a^{2} + b^{2} = c^{2}$ B、 $∠ A + ∠ B = ∠ C$ C、 $a : b : c = 3 : 4 : 5$ D、 $∠ A : ∠ B : ∠ C = 3 : 4 : 5$

查看试题解析
3. 如图，在 $Δ A B C$ 中， $B C$ 边上的高是（）

A、 $E C$ B、 $B H$ C、 $C D$ D、 $A F$

查看试题解析
4. 已知等腰三角形的两边长分别为3和6，则它的周长等于（　　）

A、12 B、12或15 C、15 D、15或18

查看试题解析
5. 如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②AB=DE，∠B=∠E，BC=EF；③∠B=∠E，BC=EF，∠C=∠F；④AB=DE，AC=DF，∠B=∠E．其中能使△ABC≌△DEF的条件有（）

A、1组 B、2组 C、3组 D、4组

查看试题解析
6. 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（）

A、10 B、7 C、5 D、4

查看试题解析
7. 如图，将一根长为24cm的筷子，置于底面直径为5cm，高为12cm的圆柱水杯中，设筷子露在杯子外面的长度为hcm，则h的取值范围是（）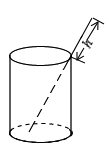

A、12cm≤h≤19cm B、12cm≤h≤13cm C、11cm≤h≤12cm D、5cm≤h≤12cm

查看试题解析
8. 如图，要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使BC=CD，再作出BF的垂线DE，使点A、C、E在同一条直线上（如图所示），可以说明△ABC≌△EDC，得AB=DE，因此测得DE的长就是AB的长，判定△ABC≌△EDC，最恰当的理由是（）

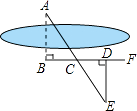A、边角边 B、角边角 C、边边边 D、边边角

查看试题解析
9. 在 $Δ A B C$ 中， $A B = 15$ ， $A C = 13$ ，高 $A D = 12$ ，则三角形的周长是（）

A、42 B、32 C、42或32 D、37或33

查看试题解析
10. 如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连结BD，BE．以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④∠ACE=∠DBC其中结论正确的个数有（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 图中x的值为.

查看试题解析
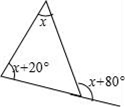12. 如图，在△ABC中，∠C＝90°，∠B＝30°，AD平分∠CAB，交BC于点D，若CD＝1，则BD＝．

查看试题解析
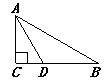13. 如图，△ABC中，∠ABC=50^° ， ∠ACB=70^° ， AD平分线∠BAC．过点D作DE⊥AB于点E，则∠ADE= .

查看试题解析
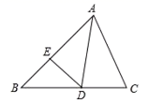14. 如图，圆柱的底面周长是14cm ，圆柱高为24cm ，一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B，那么它爬行的最短路程为.

查看试题解析
15. 如图，在已知的 $Δ A B C$ 中，按以一下步骤作图：①分别以 $B ， C$ 为圆心，大于 $\frac{1}{2} B C$ 的长为半径作弧，相交于两点 $M ， N$ ；②作直线 $M N$ 交 $A B$ 于点D，连接 $C D$ .若 $C D = A C$ ， $∠ A = 50 °$ ，则 $∠ A C B$ 的度数为.

查看试题解析
16. 如图，△ABC三边的中线AD，BE，CF的公共点G，若 $S_{△ A B C} = 12$ ，则图中阴影部分面积是.

查看试题解析
17. 如图，将边长为 $8$ 的正方形 $A B C D$ 折叠，使点D落在 $B C$ 边的中点E处，点A落在F处，折痕为 $M N$ ，则线段 $C N$ 的长为．

查看试题解析
18. 如图，在△ABC中，∠A=64°，∠ABC和∠ACD的平分线交于点A₁ ，得∠A₁；∠A₁BC和∠A₁CD的平分线交于点A₂ ，得∠A₂；∠A₂BC和∠A₂CD的平分线交于点A₃ ，则∠A₅= ．

查看试题解析

三、解答题

19. 尺规作图，不写作法，保留作图痕迹
已知：线段a和∠α

求作：△ABC，使得AB=a ， BC=2a ， ∠ABC=∠α.

查看试题解析
20. 如图，在△ABC中，AD、AE分别是高线与角平分线，∠B＝33°，∠C＝67°，求∠EAD的度数．

查看试题解析
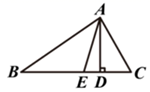21. 小明想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面.求旗杆的高度.

查看试题解析
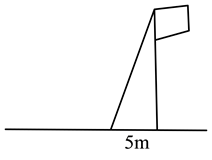22. 如图，AD∥BC，∠BAC＝70°，DE⊥AC于点E，∠D＝20°.

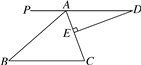(1)、求∠B的度数，并判断△ABC的形状；

(2)、若延长线段DE恰好过点B，试说明DB是∠ABC的平分线．

查看试题解析
23. 如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E，F为圆心，大于 $\frac{1}{2}$ EF长为半径作圆弧，两条圆弧交于点P，作射线AP，交CD于点M．

(1)、若∠ACD=114°，求∠MAB的度数；

(2)、若CN⊥AM，垂足为N，求证：△ACN≌△MCN．

查看试题解析
24. 如图，直线MN表示一条铁路，A，B是两个城市，它们到铁路的垂直距离分别为AA₁=20km ， BB₁=40km ，已知A₁B₁=80km ，现要在A₁ ， B₁之间设一个中转站P，使两个城市到中转站的距离之和最短，请你设计一种方案确定P点的位置，并求这个最短距离.

查看试题解析
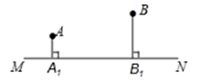25. 如图，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F．

(1)、判断BE与CF的数量关系，并说明理由；

(2)、如果AB=8，AC=6，求AE、BE的长．

查看试题解析
26. 已知点C为线段AB上一点，分别以AC、BC为边在线段AB的同侧作△ACD和△BCE，且CA=CD，CB=CE，∠ACD=∠BCE，直线AE与BD交于点F．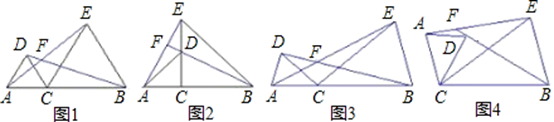

(1)、如图1，若∠ACD=60°，则∠AFB= ，如图2，若∠ACD=90°，则∠AFB= ，如图3，若∠ACD=α，则∠AFB=（用含α的式子表示）；

(2)、设∠ACD=α，将图3中的△ACD绕点C顺时针旋转任意角度（交点F至少在BD、AE中的一条线段上），如图4，试探究∠AFB与α的数量关系，并予以说明．

查看试题解析