江西省宜春市高安市2019-2020学年七年级上学期数学期中试卷

试卷更新日期：2020-09-28 类型：期中考试

进入出卷网下载

一、单选题

1. $- \frac{1}{2}$ 的倒数是（）

A、 $- 2$ B、 $\frac{1}{2}$ C、 $2$ D、 $1$

查看试题解析
2. 夏新同学上午卖废品收入13元，记为+13元，下午买旧书支出9元，记为（）元.

A、+4 B、﹣9 C、﹣4 D、+9

查看试题解析
3. 2019年“十一”黄金周期间（7天），北京市接待旅游总人数为920.7万人次，旅游总收入111.7亿元。其中920.7万用科学记数法表示为（　　）

A、 $920.7 \times 10^{4}$ B、 $92.07 \times 10^{5}$ C、 $9.207 \times 10^{5}$ D、 $9.207 \times 10^{6}$

查看试题解析
4. 下列计算正确的是（）

A、 $7 a + a = 7 a^{2}$ B、 $3 x^{2} y - 2 y x^{2} = x^{2} y$ C、 $5 y - 3 y = 2$ D、 $3 a + 2 b = 5 a b$

查看试题解析
5. 有理数 $a$ ， $b$ 在数轴上的位置如图所示，下面结论正确的是（）

A、 $b - a < 0$ B、 $a b > 0$ C、 $a + b > 0$ D、 $| a | > | b |$

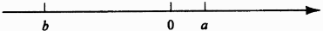查看试题解析
6. 下列说法正确的有（    ）个
①一个数前面加上“－”号，这个数就是负数    ②单项式 $\frac{3}{2} π x^{2} y$ 的系数是 $\frac{3}{2}$

③若a是正数，则-a不一定是负数    ④零既不是正数也不是负数

⑤多项式 $x^{3} y - 2 x y - 4 y - 2^{3}$ 是四次四项式，常数项是-6     ⑥零是最小的整数

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. 用四舍五入法对23.96取近似值，其中精确到十分位的是．

查看试题解析
8. 下列各式： $1 - 3 x^{2}$ ， $\frac{x}{2}$ ， $\frac{2}{x}$ ， $π - \frac{1}{4} x^{3}$ ，0， $- x^{2} + 2 x - 1$ 中整式有个．

查看试题解析
9. 代数式 $4 x^{6} y$ 与 $x^{2 n} y$ 是同类项，则常数n的值为．

查看试题解析
10. 已知 $| x | = 6$ ， $| y | = 5$ ，且 $x > y$ ，则 $2 x + y$ 值为．

查看试题解析
11. 意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，请根据这组数的规律写出第10个数是．

查看试题解析
12. 如果代数式 $- 2 a^{2} + 3 b + 8$ 的值为2，那么代数式 $- 4 a^{2} + 6 b + 12$ 的值等于．

查看试题解析

三、解答题

13. 计算：

(1)、 $- 8 + 2.5 + 6 + 1.5$

(2)、 $(- 8) \times (- 2) - 16 \div (- 4)$

查看试题解析
14. 计算： $| - 2^{2} - 3 | - (- 3^{2}) \div (- 3)$

查看试题解析
15. 化简下列各式：

(1)、 $2 a^{2} - 3 a^{2} + 5 a^{2}$

(2)、 $(- b + 3 a) + (b - a)$

查看试题解析
16. 化简： $3 (a^{2} b + 2 b) - 2 (a^{2} b - 3 b)$

查看试题解析
17. 先化简，再求值： $3 (y + 7 x y) - 4 (5 x y - y) - 6 y$ ，其中 $x = 2019$ ， $y = 1$

查看试题解析
18. 小红某星期微信收发红包记录如下：收到22.9元，发出9.9元，收到8.8元，发出35.5元，收到3.7元，发出6.6元，收到4.8元，这时她的微信钱包里的数量是增加了还是减少了？增加或减少了多少钱？

查看试题解析
19. 一条隧道的横截面如图所示，它的上部是一个半径为r的半圆，下部是一个长方形，长方形的一边长为2.5米，隧道横截面为S平方米．

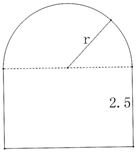(1)、用r的代数式表示S；

(2)、当 $r = 2$ 时，求S的值．（ $π$ 取3.14 ）

查看试题解析
20. 有理数x ， y在数轴上对应点如图所示：

(1)、在数轴上表示﹣x ， |y|；

(2)、试把x ， y ， 0，﹣x ， |y|这五个数从小到大用“＜”号连接，

(3)、化简：|x+y|﹣|y﹣x|+|y|.

查看试题解析
21. 已知关于x的整式 $(| k | - 3) x^{3} + (k - 3) x^{2} - k$ ．

(1)、若此整式是单项式，求k的值；

(2)、若此整式是二次多项式，求k的值；

(3)、若此整式是二项式，求k的值．

查看试题解析
22. 定义：若 $A - B = 1$ ，则称A与B是关于1的单位数，但B与A不是关于1的单位数.

(1)、3与是关于1的单位数， $x - 3$ 与是关于1的单位数（填一个含x的式子）.

(2)、若 $A = 3 (x^{2} + 2 x) - 1$ ， $B = 2 (\frac{3}{2} x^{2} + 3 x - 1)$ ，判断A与B是否是关于1 的单位数，并说明理由.

查看试题解析
23. 如图，在数轴上A点表示数a，B点表示数b，C点表示数c，已知数b是最小的正整数，且a、c满足 $| a + 2 | + {(c - 7)}^{2} = 0$ ．

(1)、a= ， b= ， c=；

(2)、若将数轴折叠，使得点A与点C重合，则点B与数表示的点重合；

(3)、点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为 $A B$ ，点A与点C之间的距离表示为 $A C$ ，点B与点C之间的距离表示为 $B C$ ，求 $A B$ 、 $A C$ 、 $B C$ 的长（用含t的式子表示）；

(4)、在（3）的条件下， $3 B C - 2 A B$ 的值是否随着时间t的变化而改变？若改变，请说明理由；若不变，请求其值．

查看试题解析