江西省九江市2019-2020学年七年级上学期数学期中试卷
试卷更新日期:2020-09-28 类型:期中考试
一、单选题
-
1. 如果收入25元记作+25元,那么支出20元记作( )元A、+5 B、+20 C、-5 D、-202. 据报道:在2019年10月1日,参加北京天安门国庆阅兵和群众“同心共筑中国梦”为主题游行的人数达到11.5万多人,11.5万用科学记数法表示为( )A、 B、 C、 D、3. 下列选项中的图形,绕其虚线旋转一周能得到下边的几何体的是( )
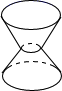 A、
A、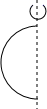 B、
B、 C、
C、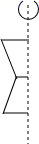 D、
D、 4. 下列运算中,正确的是( )A、-2-1=-1 B、-2(x-3y)=-2x+3y C、3÷6× =3÷3=1 D、5x2-2x2=3x25. 已知下图为一几何体的从三个不同方向看的形状图,若从正面看的长方形的长为 ,从上面看的等边三角形的边长为 ,则这个几何体的侧面积是( )
4. 下列运算中,正确的是( )A、-2-1=-1 B、-2(x-3y)=-2x+3y C、3÷6× =3÷3=1 D、5x2-2x2=3x25. 已知下图为一几何体的从三个不同方向看的形状图,若从正面看的长方形的长为 ,从上面看的等边三角形的边长为 ,则这个几何体的侧面积是( ) A、 B、 C、 D、6. 现有四种说法:①-a表示负数;②若 ,则 ;③绝对值最小的有理数是0;④ 是5次单项式.其中正确的有( )个.A、1 B、2 C、3 D、47. 有理数a、b在数轴上的位置如图所示,下列选项正确的是( )
A、 B、 C、 D、6. 现有四种说法:①-a表示负数;②若 ,则 ;③绝对值最小的有理数是0;④ 是5次单项式.其中正确的有( )个.A、1 B、2 C、3 D、47. 有理数a、b在数轴上的位置如图所示,下列选项正确的是( )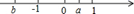 A、 B、 C、 D、8. 已知 , , …,若 ,(m,n为正整数),则m+n的值为( )A、86 B、88 C、89 D、90
A、 B、 C、 D、8. 已知 , , …,若 ,(m,n为正整数),则m+n的值为( )A、86 B、88 C、89 D、90二、填空题
-
9. 单项式 的系数是.10. 计算: .11. 图1和图2中所有的正方形都相同,将图1的正方形放在图2中的(从①、②、③、④中选填所有可能)位置,所组成的图形能够围成正方体.
 12. 下列数中,是整数的有:.
12. 下列数中,是整数的有:.+1,-3.1,0,2.5,-17,
13. 一个棱柱有12个顶点,所有的侧棱长的和是48cm,则每条侧棱长是.14. 有一个数值转换器,其工作原理如图所示,若输入-2,则输出的结果是.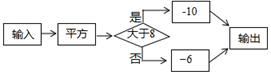 15. 已知 ,则整式 .16. 如图,数轴上每相邻两刻度之间的距离为1个单位长度,如果点B表示的数的绝对值是点A表示的数的绝对值的3倍,那么点A表示的数是.
15. 已知 ,则整式 .16. 如图,数轴上每相邻两刻度之间的距离为1个单位长度,如果点B表示的数的绝对值是点A表示的数的绝对值的3倍,那么点A表示的数是.
三、解答题
-
17. 计算:18. 先化简,再求值: ,其中 .19. 我校甲、乙、丙三位同学给希望工程捐款,已知甲同学捐款x元,乙同学的捐款金额比甲同学捐款金额的3倍少8元,丙同学的捐款金额是甲、乙两同学捐款总金额的 ,用含x的代数式表示甲、乙、丙三位同学的捐款总金额.20. 一个几何体由大小相同的小立方块搭建而成,从上面看到的几何体形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请在下面网格图中分别画出从正面和从左面看到的这个几何体的形状图.
 21. 小明、小兵、小英三人的家和学校在同一条东西走向的大街上,星期天班主任到这三位学生家进行家访,班主任从学校出发先向东走0.5千米到小明家,后又向东走1.5千米到小兵家,再向西走5千米到小英家,最后回到学校。(1)、以学校为原点,画出数轴并在数轴上分别表示出小明、小兵、小英三人家的位置。(2)、小明家距离小英家多远?(3)、这次家访,班主任共走了多少千米路程?22.(1)、若 ,则a=.(2)、若 , 与4互为相反数,求: 的值.23. 用三角形和六边形按如图所示的规律拼图案.
21. 小明、小兵、小英三人的家和学校在同一条东西走向的大街上,星期天班主任到这三位学生家进行家访,班主任从学校出发先向东走0.5千米到小明家,后又向东走1.5千米到小兵家,再向西走5千米到小英家,最后回到学校。(1)、以学校为原点,画出数轴并在数轴上分别表示出小明、小兵、小英三人家的位置。(2)、小明家距离小英家多远?(3)、这次家访,班主任共走了多少千米路程?22.(1)、若 ,则a=.(2)、若 , 与4互为相反数,求: 的值.23. 用三角形和六边形按如图所示的规律拼图案. (1)、第4个图案中,三角形有个,六边形有个;(2)、第n(n为正整数)个图案中,三角形与六边形各有多少个?(3)、第2019个图案中,三角形与六边形共有多少个?(4)、是否存在某个符合上述规律的图案,其中有100个三角形与48个六边形?如果有,指出是第几个图案;如果没有,说明理由.24. 如图A在数轴上对应的数为-2.
(1)、第4个图案中,三角形有个,六边形有个;(2)、第n(n为正整数)个图案中,三角形与六边形各有多少个?(3)、第2019个图案中,三角形与六边形共有多少个?(4)、是否存在某个符合上述规律的图案,其中有100个三角形与48个六边形?如果有,指出是第几个图案;如果没有,说明理由.24. 如图A在数轴上对应的数为-2. (1)、点B在点A右边距离A点4个单位长度,则点B所对应的数是.(2)、在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.(3)、在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
(1)、点B在点A右边距离A点4个单位长度,则点B所对应的数是.(2)、在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.(3)、在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.