江西省抚州市乐安县2019-2020学年七年级上学期数学期中试卷

试卷更新日期：2020-09-28 类型：期中考试

进入出卷网下载

一、单选题

1. $- \frac{1}{3}$ 的绝对值是（）

A、 $3$ B、 $- 3$ C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 据统计，今年春节期间（除夕到初五），微信红包总收发次数达321亿次，几乎覆盖了全国75%的网民，数据“321亿”用科学记数法可表示为（　　）

A、3.21×10⁸ B、321×10⁸ C、321×10⁹ D、3.21×10¹⁰

查看试题解析
3. 下列计算错误的是（）

A、 ${(- \frac{1}{4})}^{2} = \frac{1}{16}$ B、 $8 \div \frac{1}{10} \times 5 = 16$ C、 $- 3^{2} \times \frac{1}{9} = - 1$ D、 $4 - (- 5) \times 3 = 19$

查看试题解析
4. 给出下列判断：①单项式5×10³x²y的系数是5；②x﹣2xy+y是二次三项式；③多项式﹣3a²b+7a²b²﹣2ab+1的次数是9；④几个有理数相乘，当负因数有奇数个时，积为负.其中判断正确的是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 已知当 $x = 1$ 时， $2 a x^{2} + b x$ 的值为3，则当 $x = - 2$ 时， $a x^{2} - b x$ 的值为（）

A、－6 B、6 C、－3 D、3

查看试题解析
6. 用字母表示如图所示的阴影部分的面积是（）

A、 $b (a + b) - \frac{1}{4} π (a^{2} + b^{2})$ B、 $b (a + b) - \frac{1}{2} π (a^{2} + b^{2})$ C、 $a b - \frac{1}{2} π (a^{2} + b^{2})$ D、 $a b - \frac{1}{4} π (a^{2} + b^{2})$

查看试题解析

二、填空题

7. 在－42，＋0.01，π，0，120这5个数中，正有理数是．

查看试题解析
8. 某校去年初一招收新生x人，今年比去年增加20％，用代数式表示今年该校初一学生人数为人.

查看试题解析
9. 如图，填在各方格中的三个数之间均具有相同的规律，根据此规律，n的值是.

查看试题解析
10. 如果a和b互为相反数，c和d互为倒数，那么7cd-a-b＝．

查看试题解析
11. 如图所示，是一正方体的表面展开图，且已知其任意相对的两个面的数字和为5，那么a﹣b+c= ．

查看试题解析
12. 若 $- 2 a^{m} b^{2}$ 与 $5 a^{3} b^{n}$ 可以合并为一项，则 $m - n =$ .

查看试题解析

三、解答题

13. 计算

(1)、 $- 20 + (- 15) - (- 28) - 17$ ；

(2)、 $- 3^{2} \div {(- 3)}^{2} + 3 \times (- 2) + | - 4 |$ .

查看试题解析
14. 图①是由一些棱长都为 $1 cm$ 的小正方体组合成的简单几何体.

(1)、该几何体的表面积（含下底面）为；

(2)、该几何体的主视图如图②所示，请在下面方格纸中分别画出它的左视图和俯视图.

查看试题解析
15. 某天早上，一辆交通巡逻车从A地出发，在东西向的马路上巡视，中午到达B地，如果规定向东行驶为正，向西行驶为负，行驶纪录如下：（单位：km）
第一次
第二次
第三次
第四次
第五次
第六次
第七次
+15
－8
+6
+12
－4
+5
－10

(1)、B地在A地哪个方向，与A地相距多少千米？

(2)、巡逻车在巡逻过程中，离开A地最远是多少千米？

(3)、若每km耗油0.1升，问共耗油多少升？

查看试题解析
16. $9 \frac{14}{15} \times (- 15)$ ；

查看试题解析
17. $5 a^{2} - 2 a b - 2 (3 a^{2} + 4 a b - \frac{1}{2} b^{2})$ .

查看试题解析
18. 先化简再求值：（5x²﹣3y²）﹣[（5x²﹣2xy﹣y²）﹣（x²﹣2xy+3y²）]，其中x＝2，y＝﹣1.

查看试题解析
19. 用小立方块搭成一个几何体，从正面看和从上面看所得的平面图形如图所示，搭建这样的几何体最多要几个小立方块？最少要几个小立方块？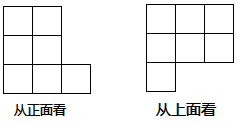

查看试题解析
20. 已知a，b满足 ${(a - 4)}^{2} + | 2 b + 3 | = 0$ .

(1)、求a，b的值；

(2)、在如图所示的数轴上将a，b，-a，-b表示出来，并用“﹤”将它们连接起来.

查看试题解析
21. 某服装厂生产一种围巾和手套，每条围巾的定价为50元，每双手套的定价为20元厂家在开展促销活动期间，向客户提供两种优惠方案：
方案①：买一条围巾送一双手套；

方案②：围巾和手套都按定价的 $80 %$ 付款.

现某客户要到该服装厂购买围巾20条，手套x双（ $x > 20$ ）.

(1)、若该客户按方案①购买，则需付款元（用含x的代数式表示）；
若该客户按方案②购买，则需付款元（用含x的代数式表示）；

(2)、若 $x = 30$ ，通过计算说明按哪种方案购买较便宜.

查看试题解析
22. 如图，将一张正方形纸片剪成四张大小一样的小正方形纸片，然后将其中一张正方形纸片再按同样方法剪成四张小正方形纸片，再将其中一张剪成四张小正方形纸片，如此进行下去.

(1)、填表：

剪的次数

1

2

3

4

5

纸片张数

4

7

(2)、如果剪了100次，共剪出多少张纸片？

(3)、如果剪了 $n$ 次，共剪出多少张纸片？

(4)、能否剪若干次后共得到2019张纸片？若能，请直接写出相应剪的次数；若不能，请说明理由.

查看试题解析
23. 历史上的数学巨人欧拉最先把关于 $x$ 的多项式用记号 $f (x)$ 的形式来表示（f可用其它字母，但不同的字母表示不同的多项式），例如 $f (x) = x^{2} + 3 x - 5$ ，把 $x = a$ 时的多项式的值用 $f (a)$ 来表示.例如 $x = - 1$ 时多项式 $x^{2} + 3 x - 5$ 的值记为 $f (- 1) = {(- 1)}^{2} + 3 \times (- 1) - 5 = - 7$ .
已知： $g (x) = - 2 x^{2} - 3 x + 1$ ， $h (x) = a x^{2} + x - 10$ .

(1)、求 $g (- 3)$ 的值；

(2)、若 $h (2) = 0$ ，求 $g (a)$ 的值.

(3)、若 $g (x) + h (x)$ 的值不含 $x^{2}$ 项，求a的值.

查看试题解析

第一次	第二次	第三次	第四次	第五次	第六次	第七次
+15	－8	+6	+12	－4	+5	－10

剪的次数	1	2	3	4	5
纸片张数	4	7