内蒙古自治区呼和浩特市2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-28 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,AB为⊙O的弦,AB=8,OC⊥AB于点D,交⊙O于点C,且CD=1,则⊙O的半径为( )
2. 如图,AB为⊙O的弦,AB=8,OC⊥AB于点D,交⊙O于点C,且CD=1,则⊙O的半径为( )
 A、8.5 B、7.5 C、9.5 D、83. 在二次函数y=x2-2x-3中,当0≤x≤3时,y的最大值和最小值分别是 ( )
A、8.5 B、7.5 C、9.5 D、83. 在二次函数y=x2-2x-3中,当0≤x≤3时,y的最大值和最小值分别是 ( )
A、0,-4 B、0,-3 C、-3,-4 D、0,04. 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为:( )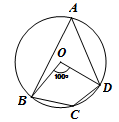 A、50° B、80° C、100° D、130°5. 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
A、50° B、80° C、100° D、130°5. 某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:x
…
﹣2
﹣1
0
1
2
…
y
…
﹣11
﹣2
1
﹣2
﹣5
…
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A、﹣11 B、﹣2 C、1 D、﹣56. 在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线 ,则原抛物线的解析式是( )A、 B、 C、 D、7. 如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b-1)x+c的图象可能是( )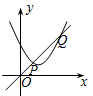 A、
A、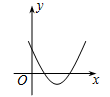 B、
B、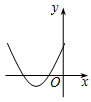 C、
C、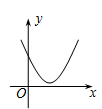 D、
D、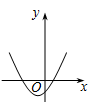 8. 如图,将△ABC绕顶点A顺时针旋转60°后,得到△AB'C',且C'为BC的中点,则C'D:DB'=( )
8. 如图,将△ABC绕顶点A顺时针旋转60°后,得到△AB'C',且C'为BC的中点,则C'D:DB'=( )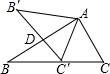 A、 B、 C、 D、9. 如图,已知二次函数 ( )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b<0;③ ;④ ;其中正确的结论是( )
A、 B、 C、 D、9. 如图,已知二次函数 ( )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b<0;③ ;④ ;其中正确的结论是( )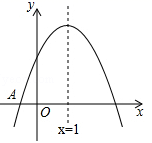 A、①③④ B、①②③ C、①②④ D、①②③④
A、①③④ B、①②③ C、①②④ D、①②③④二、填空题
-
10. 已知一元二次方程 的两根 , ,则 .11. 已知四个二次函数的图象如图所示,那么a1 , a2 , a3 , a4的大小关系是 . (请用“>”连接排序)
 12. 点 , 在二次函数 的图像上,若 , ,则 (填“>”,“=”或“<”)13. 已知抛物线 经过点 .设点 ,请在抛物线的对称轴上确定一点 ,使得 的值最大,则 点的坐标为 .14. 已知x=﹣1是一元二次方程ax2+bx﹣10=0的一个解,且a≠﹣b,则 的值为 .15. 一条弦的弦心距等于它所在圆的直径的 ,则这条弦所对的圆周角为 .16.
12. 点 , 在二次函数 的图像上,若 , ,则 (填“>”,“=”或“<”)13. 已知抛物线 经过点 .设点 ,请在抛物线的对称轴上确定一点 ,使得 的值最大,则 点的坐标为 .14. 已知x=﹣1是一元二次方程ax2+bx﹣10=0的一个解,且a≠﹣b,则 的值为 .15. 一条弦的弦心距等于它所在圆的直径的 ,则这条弦所对的圆周角为 .16.如图,P是等边三角形ABC中的一个点,PA=2,PB=2 , PC=4,则三角形ABC的边长为

三、解答题
-
17. 解方程:(1)、2x2﹣4x﹣1=0.(2)、(x+1)2=6x+6.18. 李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.(1)、要使这两个正方形的面积之和等于58 cm2 , 李明应该怎么剪这根铁丝?(2)、李明认为这两个正方形的面积之和不可能等于48 cm2 , 你认为他的说法符合题意吗?请说明理由.19. 某隧道洞的内部截面顶部是抛物线形,现测定地面宽 ,隧道顶点 到地面 的距离为 ,(1)、建立适当的平面直角坐标系,并求该抛物线的解析式;(2)、一辆小轿车长4.5米,宽2米,高1.5米,同样大小的小轿车通过该隧道,最多能有几辆车并行?20. 新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?21. 在正方形ABCD中,∠EDF=45°,求证:EF=AE+CF .
 22. 已知关于 的一元二次方程 .(1)、求证:方程有两个不相等的实数根.(2)、如果方程的两实数根为 ,且 ,求 的值.23. 已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,
22. 已知关于 的一元二次方程 .(1)、求证:方程有两个不相等的实数根.(2)、如果方程的两实数根为 ,且 ,求 的值.23. 已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,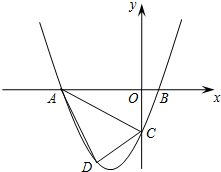 (1)、求抛物线的解析式;(2)、若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.24. 如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC .
(1)、求抛物线的解析式;(2)、若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.24. 如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC . (1)、若∠DFC=40º,求∠CBF的度数.(2)、求证: CD⊥DF .25.
(1)、若∠DFC=40º,求∠CBF的度数.(2)、求证: CD⊥DF .25.如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D
 (1)、求二次函数的表达式。
(1)、求二次函数的表达式。
(2)、在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标(3)、有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从 点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.