内蒙古自治区鄂尔多斯市准格尔旗2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-28 类型:期中考试
一、单选题
-
1. 一元二次方程 的根是( )A、 B、 C、3或0 D、0或-32. 下列图案中既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若点A(3-m,n+2)关于原点的对称点B的坐标是(-3,2),则m,n的值为( )A、m=-6,n=-4 B、m=O,n=-4 C、m=6,n=4 D、m=6,n=-44. 用配方法解方程x2﹣2x﹣5=0时,原方程应变形为( )A、(x+1)2=6 B、(x+2)2=9 C、(x﹣1)2=6 D、(x﹣2)2=95. 二次函数 的图象与x轴有交点,则k的取值范围是( )A、 B、 且 C、 D、 且6. 将抛物线y= x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为( )A、y= (x﹣8)2+5 B、y= (x﹣4)2+5 C、y= (x﹣8)2+3 D、y= (x﹣4)2+37. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
3. 若点A(3-m,n+2)关于原点的对称点B的坐标是(-3,2),则m,n的值为( )A、m=-6,n=-4 B、m=O,n=-4 C、m=6,n=4 D、m=6,n=-44. 用配方法解方程x2﹣2x﹣5=0时,原方程应变形为( )A、(x+1)2=6 B、(x+2)2=9 C、(x﹣1)2=6 D、(x﹣2)2=95. 二次函数 的图象与x轴有交点,则k的取值范围是( )A、 B、 且 C、 D、 且6. 将抛物线y= x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为( )A、y= (x﹣8)2+5 B、y= (x﹣4)2+5 C、y= (x﹣8)2+3 D、y= (x﹣4)2+37. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )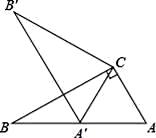 A、30° B、60° C、90° D、150°8. 如图,抛物线 与x轴一个交点为 ,对称轴为直线 ,则 时x的范围是
A、30° B、60° C、90° D、150°8. 如图,抛物线 与x轴一个交点为 ,对称轴为直线 ,则 时x的范围是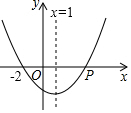 A、 或 B、 C、 D、9. 有一座抛物线形拱桥,正常水位桥下面宽度为 米,拱顶距离水平面 米,如图建立直角坐标系,若正常水位时,桥下水深 米,为保证过往船只顺利航行,桥下水面宽度不得小于 米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
A、 或 B、 C、 D、9. 有一座抛物线形拱桥,正常水位桥下面宽度为 米,拱顶距离水平面 米,如图建立直角坐标系,若正常水位时,桥下水深 米,为保证过往船只顺利航行,桥下水面宽度不得小于 米,则当水深超过多少米时,就会影响过往船只的顺利航行( ) A、 B、 C、 D、10. 若二次函数 ,当 分别取 两个不同的值时,函数值相等,则当 取 时,函数值为( )A、1 B、-1 C、2 D、-2
A、 B、 C、 D、10. 若二次函数 ,当 分别取 两个不同的值时,函数值相等,则当 取 时,函数值为( )A、1 B、-1 C、2 D、-2二、填空题
-
11. 若一元二次方程 有一根为 ,则 .12. 点A(﹣3,y1),B(2,y2),C(3,y3)在抛物线y=2x2﹣4x+c上,则y1 , y2 , y3的大小关系是 .13. 如图,已知 ,现将 点绕原点 逆时针旋转 得到 ,则 的坐标是 .
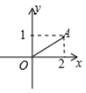 14. 某药品原价每盒25元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒16元,则该药品平均每次降价的百分率是 .15. 如图,在菱形 中, ,将菱形 绕点 逆时针方向旋转,对应得到菱形 ,点 在 上, 与 交于点 ,则 的长是 .
14. 某药品原价每盒25元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒16元,则该药品平均每次降价的百分率是 .15. 如图,在菱形 中, ,将菱形 绕点 逆时针方向旋转,对应得到菱形 ,点 在 上, 与 交于点 ,则 的长是 . 16. 二次函数 的图象如图所示,对称轴是 .下列结论:
16. 二次函数 的图象如图所示,对称轴是 .下列结论:① ;② ;③ ;④ .
其中正确的是 .
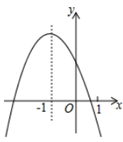
三、解答题
-
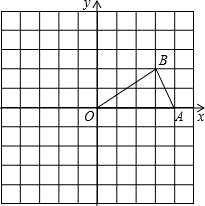
17. 解下列方程:(1)、(2)、18. 如图,已知点A , B的坐标分别为(4,0),(3,2).
 (1)、画出△AOB关于原点O对称的图形△COD;(2)、将△AOB绕点O按逆时针方向旋转90°得到△EOF , 画出△EOF;(3)、点D的坐标是 , 点F的坐标是 , 此图中线段BF和DF的关系是 .19. 世博会中国国家馆的平面示意图如图,其外框是一个大正方形,中间四个全等的小正方形(阴影部分)是支撑展馆的核心简,标记了字母的五个全等的正方形是展厅,已知核心简的边长比展厅的边长的一半多一米,外框的面积刚好是四个核心简面积和的 倍,求核心简的边长.
(1)、画出△AOB关于原点O对称的图形△COD;(2)、将△AOB绕点O按逆时针方向旋转90°得到△EOF , 画出△EOF;(3)、点D的坐标是 , 点F的坐标是 , 此图中线段BF和DF的关系是 .19. 世博会中国国家馆的平面示意图如图,其外框是一个大正方形,中间四个全等的小正方形(阴影部分)是支撑展馆的核心简,标记了字母的五个全等的正方形是展厅,已知核心简的边长比展厅的边长的一半多一米,外框的面积刚好是四个核心简面积和的 倍,求核心简的边长.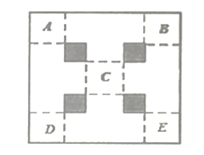 20. 某商场将每件进价为80元的某种商品按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.(1)、若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?(2)、设后来该商品每件降价x元,商场一天可获利润y元.求出y与x之间的函数关系式,并求当x取何值时,商场获利润最大?21. 已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
20. 某商场将每件进价为80元的某种商品按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.(1)、若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?(2)、设后来该商品每件降价x元,商场一天可获利润y元.求出y与x之间的函数关系式,并求当x取何值时,商场获利润最大?21. 已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.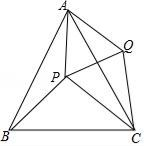 (1)、求证:PB=QC;(2)、若PA=3,PB=4,∠APB=150°,求PC的长度.22. 在 中, ,点 从 点开始沿着 边向点 以 的速度移动,点 从 点开始沿 边向点 以 的速度移动,如果 分别从 同时出发,如果运动时间为 秒.
(1)、求证:PB=QC;(2)、若PA=3,PB=4,∠APB=150°,求PC的长度.22. 在 中, ,点 从 点开始沿着 边向点 以 的速度移动,点 从 点开始沿 边向点 以 的速度移动,如果 分别从 同时出发,如果运动时间为 秒. (1)、 为何值时, 间的距离等于 ?(2)、 为何值时, 有最大值?最大值是多少?23. 如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)、 为何值时, 间的距离等于 ?(2)、 为何值时, 有最大值?最大值是多少?23. 如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.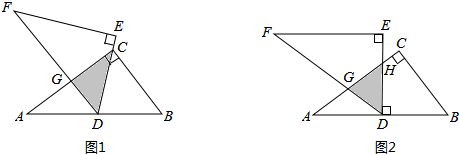 (1)、若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;(2)、合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.24. 已知,抛物线 与 轴交于点 ,与 轴交于 , 两点,点 在点 左侧.点 的坐标为 , .
(1)、若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;(2)、合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.24. 已知,抛物线 与 轴交于点 ,与 轴交于 , 两点,点 在点 左侧.点 的坐标为 , . (1)、求抛物线的解析式;(2)、当 时,如图所示,若点 是第三象限抛物线上方的动点,设点 的横坐标为 ,三角形 的面积为 ,求出 与 的函数关系式,并直接写出自变量 的取值范围;请问当 为何值时, 有最大值?最大值是多少.
(1)、求抛物线的解析式;(2)、当 时,如图所示,若点 是第三象限抛物线上方的动点,设点 的横坐标为 ,三角形 的面积为 ,求出 与 的函数关系式,并直接写出自变量 的取值范围;请问当 为何值时, 有最大值?最大值是多少.