内蒙古自治区赤峰市翁牛特旗2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-28 类型:期中考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列关于x的方程有实数根的是( )A、 B、 C、 D、3.
2. 下列关于x的方程有实数根的是( )A、 B、 C、 D、3.已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
 A、﹣1<x<3 B、﹣1<x<4 C、x<﹣1或x>3 D、x<﹣1或x>44. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、5. 根据下列表格中的对应值,判断 y = ax 2 + bx + c ( a ≠0, a 、 b 、 c 为常数)与 x 轴的交点的横坐标的取值范围是( )
A、﹣1<x<3 B、﹣1<x<4 C、x<﹣1或x>3 D、x<﹣1或x>44. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、5. 根据下列表格中的对应值,判断 y = ax 2 + bx + c ( a ≠0, a 、 b 、 c 为常数)与 x 轴的交点的横坐标的取值范围是( )x
3.23
3.24
3.25
3.26
y = ax 2 + bx + c
-0.69
-0.02
0.03
0.36
A、0< x <3.23 B、3.23< x <3.24 C、3.24< x <3.25 D、3.25< x <3.266. 二次函数y= (x-4)2+5的图象的开口方向、对称轴、顶点坐标分别是( )A、向上,直线x=4,(4,5) B、向上,直线x=-4,(-4,5) C、向上,直线x=4,(4,-5) D、向下,直线x=-4,(-4,5)7. 已知二次函数y=3(x﹣1)2+k的图象上有三点A( ,y1),B(2,y2),C(﹣ ,y3),则y1、y2、y3的大小关系为( )A、y1>y2>y3 B、y2>y1>y3 C、y3>y1>y2 D、y3>y2>y18. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根为0,则a值为( )A、1 B、﹣1 C、±1 D、09. 某种商品零售价经过两次降价后的价格为降价前的81%,则平均每次降价( )A、10% B、19% C、9.5% D、20%10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②4a+2b+c>0;③2a+b=0;④b2>4ac; ⑤ 3a+c>0.其中正确的结论的有( )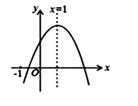 A、2个 B、3个 C、4个 D、5个11. 将抛物线y=2x2向左平移3个单位得到的抛物线的解析式是( )A、y=2x2+3 B、y=2x2﹣3 C、y=2(x+3)2 D、y=2(x﹣3)212. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )
A、2个 B、3个 C、4个 D、5个11. 将抛物线y=2x2向左平移3个单位得到的抛物线的解析式是( )A、y=2x2+3 B、y=2x2﹣3 C、y=2(x+3)2 D、y=2(x﹣3)212. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )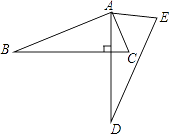 A、60° B、75° C、85° D、90°13. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、
A、60° B、75° C、85° D、90°13. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、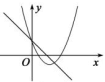 B、
B、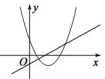 C、
C、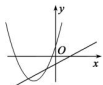 D、
D、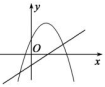 14. 定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax2+bx+c=0(a≠0)满足a﹣b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是( )A、方有两个相等的实数根 B、方程有一根等于0 C、方程两根之和等于0 D、方程两根之积等于0
14. 定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax2+bx+c=0(a≠0)满足a﹣b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是( )A、方有两个相等的实数根 B、方程有一根等于0 C、方程两根之和等于0 D、方程两根之积等于0二、填空题
-
15. 若点P(m,2)与点Q(3,n)关于原点对称,则m﹣n=.16. 若一元二次方程 有一根为 ,则a+b=.17. 如果抛物线y=ax2﹣2ax+c与x轴的一个交点为(5,0),那么与x轴的另一个交点的坐标是 .
18. 如图所示,用火柴棒拼成的图案,根据图案的规律,第n个图案中有根火柴棒.
三、解答题
-
19. 解方程.(1)、x2﹣14x=8(2)、3x(x﹣2)=2(2﹣x)20. 如图, 三个顶点的坐标分别为 , , 。
 (1)、请画出 关于 轴对称后得到的 ;(2)、直接写出点 ,点 ,点 的坐标;(3)、在 轴上寻找一个点 ,使 的周长最小,并直接写出 的周长的最小值。21. 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.(1)、如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;(3)、如果△ABC是等边三角形,试求这个一元二次方程的根.22. 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2 .
(1)、请画出 关于 轴对称后得到的 ;(2)、直接写出点 ,点 ,点 的坐标;(3)、在 轴上寻找一个点 ,使 的周长最小,并直接写出 的周长的最小值。21. 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.(1)、如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;(3)、如果△ABC是等边三角形,试求这个一元二次方程的根.22. 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2 .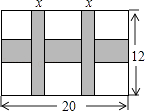 (1)、求y与x之间的函数关系式;(2)、若图案中三条彩条所占面积是图案面积的 ,求横、竖彩条的宽度.23. 惠农商场于今年五月份以每件30元的进价购进一批商品.当商品售价为40元时,五月份销售256件.六、七月该商品十分畅销.销售量持续走高.在售价不变的基础上,7月份的销售量达到400件.设六、七这两个月月平均增长率不变.(1)、求六、七这两个月的月平均增长率;(2)、从八月份起,商场采用降价促销的方式回馈顾客,经调查发现,该商品每降价0.5元,销售量增加5件,当商品降价多少元时,商场获利2640元?24. 在Rt△ABC中,AC=24cm,BC=7cm,点P在BC上从B运动到C(不包括C),速度为2cm/s;点Q在AC上从C运动到A(不包括A),速度为5cm/s.若点P,Q分别从B,C同时出发,当P,Q两点中有一个点运动到终点时,两点均停止运动.设运动时间为t秒,请解答下列问题,并写出探索的主要过程.
(1)、求y与x之间的函数关系式;(2)、若图案中三条彩条所占面积是图案面积的 ,求横、竖彩条的宽度.23. 惠农商场于今年五月份以每件30元的进价购进一批商品.当商品售价为40元时,五月份销售256件.六、七月该商品十分畅销.销售量持续走高.在售价不变的基础上,7月份的销售量达到400件.设六、七这两个月月平均增长率不变.(1)、求六、七这两个月的月平均增长率;(2)、从八月份起,商场采用降价促销的方式回馈顾客,经调查发现,该商品每降价0.5元,销售量增加5件,当商品降价多少元时,商场获利2640元?24. 在Rt△ABC中,AC=24cm,BC=7cm,点P在BC上从B运动到C(不包括C),速度为2cm/s;点Q在AC上从C运动到A(不包括A),速度为5cm/s.若点P,Q分别从B,C同时出发,当P,Q两点中有一个点运动到终点时,两点均停止运动.设运动时间为t秒,请解答下列问题,并写出探索的主要过程. (1)、当t为何值时,P,Q两点的距离为 cm?(2)、当t为何值时,△PCQ的面积为15cm2?
(1)、当t为何值时,P,Q两点的距离为 cm?(2)、当t为何值时,△PCQ的面积为15cm2?

