内蒙古包头市青山区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-28 类型:期中考试
一、单选题
-
1. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根2. 一个铁制零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( )
 A、
A、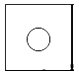 B、
B、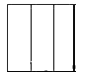 C、
C、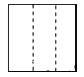 D、
D、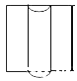 3. 两个不同长度的物体在同一时刻同一地点的太阳光下得到的投影是( )A、相等 B、长的较长 C、短的较长 D、不能确定4. 如图,有三个矩形,其中是相似图形的是( )
3. 两个不同长度的物体在同一时刻同一地点的太阳光下得到的投影是( )A、相等 B、长的较长 C、短的较长 D、不能确定4. 如图,有三个矩形,其中是相似图形的是( ) A、甲和乙 B、甲和丙 C、乙和丙 D、甲、乙和丙5. 如图,点 是反比例函数 图象上任意一点, 轴于 ,点 在 轴上, 的面积为2,则 的值为( )
A、甲和乙 B、甲和丙 C、乙和丙 D、甲、乙和丙5. 如图,点 是反比例函数 图象上任意一点, 轴于 ,点 在 轴上, 的面积为2,则 的值为( ) A、1 B、-1 C、4 D、-46. 用配方法解方程 ,变形结果正确的是( )A、 B、 C、 D、7. 如图,四边形 和 是以点 为位似中心的位似图形,若 ,四边形 的面积为9 ,则四边形 的面积为( )
A、1 B、-1 C、4 D、-46. 用配方法解方程 ,变形结果正确的是( )A、 B、 C、 D、7. 如图,四边形 和 是以点 为位似中心的位似图形,若 ,四边形 的面积为9 ,则四边形 的面积为( ) A、15 B、25 C、18 D、278. 某农机厂一月份生产零件50万个,第一季度共生产零件182万个.设该厂二、三月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x)²=182 B、50+50(1+x)+50(1+x)²=182 C、50(1+2x)=182 D、50+50(1+x)+50(1+2x)²=1829. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、10. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A、15 B、25 C、18 D、278. 某农机厂一月份生产零件50万个,第一季度共生产零件182万个.设该厂二、三月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x)²=182 B、50+50(1+x)+50(1+x)²=182 C、50(1+2x)=182 D、50+50(1+x)+50(1+2x)²=1829. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、10. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )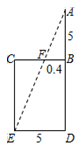 A、1.25尺 B、56.5尺 C、6.25尺 D、57.5尺11. 已知下列命题:①对角线互相垂直的四边形是菱形;②若 ,则 ;③两个位似图形一定是相似图形;④若 ,则 ;其中原命题是真命题逆命题是假命题的有( )A、1个 B、2个 C、3个 D、4个12. 如图,△ABC 是等边三角形,点 D、E 分别在 BC、AC 上,且 BD= BC,CE= AC,BE、AD 相交于点 F,连接 DE, 则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DF•DA;④AF•BE=AE•AC,正确的结论有( )
A、1.25尺 B、56.5尺 C、6.25尺 D、57.5尺11. 已知下列命题:①对角线互相垂直的四边形是菱形;②若 ,则 ;③两个位似图形一定是相似图形;④若 ,则 ;其中原命题是真命题逆命题是假命题的有( )A、1个 B、2个 C、3个 D、4个12. 如图,△ABC 是等边三角形,点 D、E 分别在 BC、AC 上,且 BD= BC,CE= AC,BE、AD 相交于点 F,连接 DE, 则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DF•DA;④AF•BE=AE•AC,正确的结论有( )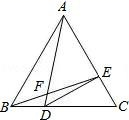 A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
13. 请给c的一个值,c=时,方程x2﹣3x+c=0无实数根.14. 如图是一个圆柱体的三视图,由图中数据计算此圆柱体的侧面积为 . (结果保留π)
 15. 地图上两地间的距离为3.5厘米,比例尺为1:1000000,那么两地间的实际距离为 千米.16. 如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为 m.
15. 地图上两地间的距离为3.5厘米,比例尺为1:1000000,那么两地间的实际距离为 千米.16. 如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为 m. 17. 已知关于 的一元二次方程 有两个实数根, 为正整数,且该方程的根都是整数,则符合条件的所有正整数 的和为 .18. 已知三个边长分别为2 ,3 ,5 的正方形如图排列,则图中阴影部分的面积为 .
17. 已知关于 的一元二次方程 有两个实数根, 为正整数,且该方程的根都是整数,则符合条件的所有正整数 的和为 .18. 已知三个边长分别为2 ,3 ,5 的正方形如图排列,则图中阴影部分的面积为 .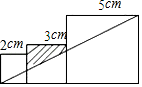 19. 如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO , 反比例函数y= (x<0)的图象经过点A , 若S△AOB= ,则k的值为 .
19. 如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO , 反比例函数y= (x<0)的图象经过点A , 若S△AOB= ,则k的值为 . 20. 如图, 中, 直线 交 于点 交 于点 交 于点 若 则 .
20. 如图, 中, 直线 交 于点 交 于点 交 于点 若 则 .
三、解答题
-
21. 解下列方程:(1)、(2)、22. 如图,四边形 中, 平分 , ; , 为 的中点,
 (1)、求证: ;(2)、 与 有怎样的位置关系?试说明理由.23. 水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.(1)、若将这种水果每斤的售价降低x元,则每天的销售量是 斤。(用含x的代数式表示)(2)、销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?24. 如图,是住宅区内的两幢楼,它们的高 ,两楼间的距离 ,现需了解甲楼对乙楼的采光的影响情况.
(1)、求证: ;(2)、 与 有怎样的位置关系?试说明理由.23. 水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.(1)、若将这种水果每斤的售价降低x元,则每天的销售量是 斤。(用含x的代数式表示)(2)、销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?24. 如图,是住宅区内的两幢楼,它们的高 ,两楼间的距离 ,现需了解甲楼对乙楼的采光的影响情况. (1)、当太阳光与水平线的夹角为 角时,求甲楼的影子在乙楼上有多高(答案可用根号表示);(2)、若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
(1)、当太阳光与水平线的夹角为 角时,求甲楼的影子在乙楼上有多高(答案可用根号表示);(2)、若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?