福建省龙岩市永定区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-28 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
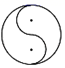 B、
B、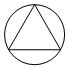 C、
C、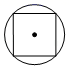 D、
D、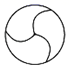 2. 下列方程属于一元二次方程的是( )A、 B、 C、 D、3. 平面直角坐标系内一点P(2,-3)关于原点对称点的坐标是( )A、(3,-2) B、(2,3) C、(-2,3) D、(2,-3)4. 二次函数y= (x-4)2+5的图象的开口方向、对称轴、顶点坐标分别是( )A、向上,直线x=4,(4,5) B、向上,直线x=-4,(-4,5) C、向上,直线x=4,(4,-5) D、向下,直线x=-4,(-4,5)5. 将一元二次方程x2﹣4x﹣7=0配方,所得的方程是( )A、(x﹣2)2=11 B、(x﹣2)2=3 C、(x+2)2=11 D、(x+2)2=36. 某厂一月份生产某机器100台,计划三月份生产144台.设二、三月份每月的平均增长率为x,根据题意列出的方程是( )A、100(1+x)2=144 B、100(1﹣x)2=144 C、144(1+x)2=100 D、144(1﹣x)2=1007. 如图,四边形ABCD内接于⊙O , 若∠BCD=110°,则∠BOD的度数为( )
2. 下列方程属于一元二次方程的是( )A、 B、 C、 D、3. 平面直角坐标系内一点P(2,-3)关于原点对称点的坐标是( )A、(3,-2) B、(2,3) C、(-2,3) D、(2,-3)4. 二次函数y= (x-4)2+5的图象的开口方向、对称轴、顶点坐标分别是( )A、向上,直线x=4,(4,5) B、向上,直线x=-4,(-4,5) C、向上,直线x=4,(4,-5) D、向下,直线x=-4,(-4,5)5. 将一元二次方程x2﹣4x﹣7=0配方,所得的方程是( )A、(x﹣2)2=11 B、(x﹣2)2=3 C、(x+2)2=11 D、(x+2)2=36. 某厂一月份生产某机器100台,计划三月份生产144台.设二、三月份每月的平均增长率为x,根据题意列出的方程是( )A、100(1+x)2=144 B、100(1﹣x)2=144 C、144(1+x)2=100 D、144(1﹣x)2=1007. 如图,四边形ABCD内接于⊙O , 若∠BCD=110°,则∠BOD的度数为( )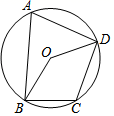 A、35° B、70° C、110° D、140°8. 过⊙O内一点M的最长弦长为10 cm , 最短弦长为8 cm , 那么OM为( )A、6 cm B、3 cm C、 cm D、9 cm9. 若函数y= +2x-b的图像与坐标轴有三个交点,则b的取值范围是( )A、b>1且b≠0 B、b<1且b≠0 C、b≤1且b≠0 D、b≥-1且b≠010. 我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2×i=(﹣1)×i=﹣i,i4=(i2)2=(﹣1)2=1,从而对任意正整数n,我们可以得到i4n+1=i4n×i=(i4)n×i=i,i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013+…+i2019的值为( )A、0 B、1 C、﹣1 D、i
A、35° B、70° C、110° D、140°8. 过⊙O内一点M的最长弦长为10 cm , 最短弦长为8 cm , 那么OM为( )A、6 cm B、3 cm C、 cm D、9 cm9. 若函数y= +2x-b的图像与坐标轴有三个交点,则b的取值范围是( )A、b>1且b≠0 B、b<1且b≠0 C、b≤1且b≠0 D、b≥-1且b≠010. 我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2×i=(﹣1)×i=﹣i,i4=(i2)2=(﹣1)2=1,从而对任意正整数n,我们可以得到i4n+1=i4n×i=(i4)n×i=i,i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013+…+i2019的值为( )A、0 B、1 C、﹣1 D、i二、填空题
-
11. 一元二次方程3x(x﹣3)=2x2﹣1化为一般形式为 .12. 在平面直角坐标系中,O为坐标原点,点A的坐标为(4,1),将OA绕原点逆时针方向旋转90°得OB,则点B的坐标为 .13. 点A(2,y1)、B(3,y2)是二次函数y=x2﹣2x+m的图象上两点,则y1与y2的大小关系为y1y2(填“>”、“<”、“=”).14. 在平面直角坐标系中,将抛物线y= 先向右平移两个单位,再向上平移两个单位,得到的抛物线关系式是.15. 如图,点 , , , 在 上, , , ,则 .
 16. 如图所示,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=6,BC=8,则BD=.
16. 如图所示,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=6,BC=8,则BD=.
三、解答题
-
17. 选用适当的方法,解下列方程:(1)、x2﹣2x﹣3=0;(2)、2x(x﹣2)=x﹣2.18. 现将进货为40元的商品按50元售出时,就能卖出500件.已知这批商品每件涨价1元,其销售量将减少10个.问为了赚取8000元利润,同时尽量照顾到顾客的利益,售价应定为多少?这时应进货多少件?19. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,﹣4)、B(3,﹣3)、C(1,﹣1)(每个小方格都是边长为一个单位长度的正方形).
 (1)、请画出△ABC关于原点对称的△A1B1C1 , 并写出A1 , B1 , C1的坐标;(2)、请画出△ABC绕点B逆时针旋转90°后的△A2B2C2 .20. 如图,已知抛物线y=x2+x﹣6与x轴两个交点分别是A、B(点A在点B的左侧).
(1)、请画出△ABC关于原点对称的△A1B1C1 , 并写出A1 , B1 , C1的坐标;(2)、请画出△ABC绕点B逆时针旋转90°后的△A2B2C2 .20. 如图,已知抛物线y=x2+x﹣6与x轴两个交点分别是A、B(点A在点B的左侧). (1)、求A、B的坐标;(2)、利用函数图象,写出y<0时,x的取值范围.21. 如图,⊙O的直径AB为10cm,弦AC为6cm,
(1)、求A、B的坐标;(2)、利用函数图象,写出y<0时,x的取值范围.21. 如图,⊙O的直径AB为10cm,弦AC为6cm,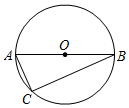 (1)、用尺规作图画出∠ACB的平分线交⊙O于点D.(不要写作法,保留作图痕迹)(2)、分别连接点AD和BD,求弦BC、AD、BD的长.22. 参与两个数学活动,再回答问题:
(1)、用尺规作图画出∠ACB的平分线交⊙O于点D.(不要写作法,保留作图痕迹)(2)、分别连接点AD和BD,求弦BC、AD、BD的长.22. 参与两个数学活动,再回答问题:活动 :观察下列两个两位数的积 两个乘数的十位上的数都是9,个位上的数的和等于 ,猜想其中哪个积最大?
, , , , , , , , .
活动 :观察下列两个三位数的积 两个乘数的百位上的数都是9,十位上的数与个位上的数组成的数的和等于 ,猜想其中哪个积最大?
, , , , , , .
(1)、分别写出在活动 、 中你所猜想的是哪个算式的积最大?(2)、对于活动 ,请用二次函数的知识证明你的猜想.23. 已知关于x的一元二次方程x2﹣x+ m=0有两个实数根.(1)、若m为正整数,求此方程的根.(2)、设此方程的两个实数根为a、b,若y=a(a﹣1)﹣2b2+2b+1,求y的取值范围.24. 如图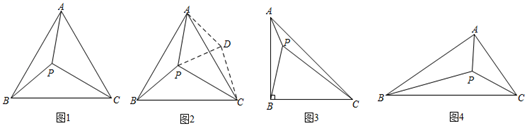 (1)、如图1,点P是等边△ABC内一点,已知PA=3,PB=4,PC=5,求∠APB的度数.
(1)、如图1,点P是等边△ABC内一点,已知PA=3,PB=4,PC=5,求∠APB的度数.分析:要直接求∠A的度数显然很因难,注意到条件中的三边长恰好是一组勾股数,因此考虑借助旋转把这三边集中到一个三角形内.
解:如图2,作∠PAD=60°使AD=AP,连接PD,CD,则△PAD是等边三角形.
∴=AD=AP=3,∠ADP=∠PAD=60°
∵△ABC是等边三角形
∴AC=AB,∠BAC=60°∴∠BAP=
∴△ABP≌△ACD
∴BP=CD=4,=∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC=°
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
(2)、如图3,在△ABC中,AB=BC,∠ABC=90°,点P是△ABC内一点,PA=1,PB=2,PC=3,求∠APB的度数.(3)、拓展应用.如图4,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC内部的任意一点,连接PA,PB,PC,则PA+PB+PC的最小值为 .25. 在平面直角坐标系 中,直线 与 轴、 轴分别交于点 , ,抛物线 经过点 ,将点 向右平移5个单位长度,得到点 .(1)、求点 的坐标;
(2)、求抛物线的对称轴;
(3)、若抛物线与线段 恰有一个公共点,结合函数图象,求 的取值范围.