福建省福州市晋安区九校联考2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-28 类型:期中考试
一、单选题
-
1. 下面是一位美术爱好者利用网格图设计的几个英文字母的图形,你认为其中既是轴对称图形又是中心对称图形的是( )A、
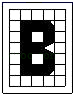 B、
B、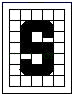 C、
C、 D、
D、 2. 二次函数 的顶点坐标是( )A、(2,3) B、(-1,-3) C、(1,3) D、(-1,2)3. 的半径为 ,若点 到圆心的距离为 ,点 在( )A、圆内 B、圆上 C、圆外 D、无法确定4. 正六边形的边心距为 ,则该正六边形的边长是( )A、 B、2 C、3 D、25. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、6. x= 是下列哪个一元二次方程的根( )A、3x2+5x+1=0 B、3x2﹣5x+1=0 C、3x2﹣5x﹣1=0 D、3x2+5x﹣1=07. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )
2. 二次函数 的顶点坐标是( )A、(2,3) B、(-1,-3) C、(1,3) D、(-1,2)3. 的半径为 ,若点 到圆心的距离为 ,点 在( )A、圆内 B、圆上 C、圆外 D、无法确定4. 正六边形的边心距为 ,则该正六边形的边长是( )A、 B、2 C、3 D、25. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、6. x= 是下列哪个一元二次方程的根( )A、3x2+5x+1=0 B、3x2﹣5x+1=0 C、3x2﹣5x﹣1=0 D、3x2+5x﹣1=07. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( ) A、8cm B、5cm C、3cm D、2cm8. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
A、8cm B、5cm C、3cm D、2cm8. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )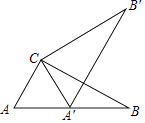 A、12 B、6 C、6 D、9. 如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为( )
A、12 B、6 C、6 D、9. 如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为( )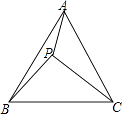 A、 B、 C、 D、10. 已知一个二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4 , 则y1 , y2 , y3 , y4的最值情况是( )A、y3最小,y1最大 B、y3最小,y4最大 C、y1最小,y4最大 D、无法确定
A、 B、 C、 D、10. 已知一个二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4 , 则y1 , y2 , y3 , y4的最值情况是( )A、y3最小,y1最大 B、y3最小,y4最大 C、y1最小,y4最大 D、无法确定二、填空题
-
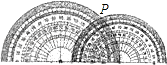
11. 点 (5,-8)关于原点对称点 的坐标为12. 方程 的根是 。13. 在一幢高125m的大楼上掉下一个苹果,苹果离地面的高度h(m)与时间t(s)大致有如下关系:h=125﹣5t2.秒钟后苹果落到地面.14. 圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是 .15. 如图,小量角器的零度线在大量角器的零度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在小量角器上对应的度数为65°,那么在大量角器上对应的度数为度(只需写出0°~90°的角度).
 16. 如图,在平面直角坐标系中,点 在抛物线 上运动,过点 作 轴于点 ,以 为对角线作矩形 连结 则对角线 的最小值为 .
16. 如图,在平面直角坐标系中,点 在抛物线 上运动,过点 作 轴于点 ,以 为对角线作矩形 连结 则对角线 的最小值为 .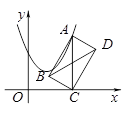
三、解答题
-
17. 解方程:(1)、(2)、18. 已知:关于x的一元二次方程x2+4x﹣m2=0(1)、若方程有一个根是1,求m的值;(2)、求证:无论m取何值时,方程总有两个不相等的实数根.19. 如图,已知 , , ,是平面直角坐示系上三点.
 (1)、请画出 关于原点对称的 ;(2)、画出 绕原点 顺时针方向旋转 后得到的 ,并写出的 坐标.20. 如图,已知在平面直角坐标系中,抛物线过点 , , .求抛物线的解析式,并求出抛物线的顶点 的坐标.
(1)、请画出 关于原点对称的 ;(2)、画出 绕原点 顺时针方向旋转 后得到的 ,并写出的 坐标.20. 如图,已知在平面直角坐标系中,抛物线过点 , , .求抛物线的解析式,并求出抛物线的顶点 的坐标. 21. 如图,已知⊙O的半径为5,直线l切⊙O于A , 在直线l上取点B , AB=4.
21. 如图,已知⊙O的半径为5,直线l切⊙O于A , 在直线l上取点B , AB=4.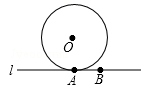 (1)、请用无刻度的直尺和圆规,过点B作直线m⊥l , 交⊙O于C、D(点D在点C的上方);(保留作图痕迹,不要求写作法)(2)、求BC的长.22. 旅行社为吸引游客组团去黄满寨风景区旅游,推出了如下收费标准:如果人数不超过25人,人均旅游费用为:1000元;如果人数超过25人,每超过1人,人均旅游费用降低20元,但人均旅游费用不低于700元.某单位组织员工去黄满寨风景区旅游,共支付给旅行社旅游费用27000元,请问:(1)、该单位旅游人数超过25人吗?说明理由.(2)、这次共有多少名员工去黄满寨风景区旅游?23. 如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.
(1)、请用无刻度的直尺和圆规,过点B作直线m⊥l , 交⊙O于C、D(点D在点C的上方);(保留作图痕迹,不要求写作法)(2)、求BC的长.22. 旅行社为吸引游客组团去黄满寨风景区旅游,推出了如下收费标准:如果人数不超过25人,人均旅游费用为:1000元;如果人数超过25人,每超过1人,人均旅游费用降低20元,但人均旅游费用不低于700元.某单位组织员工去黄满寨风景区旅游,共支付给旅行社旅游费用27000元,请问:(1)、该单位旅游人数超过25人吗?说明理由.(2)、这次共有多少名员工去黄满寨风景区旅游?23. 如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.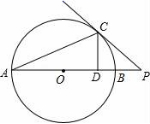 (1)、求证:CP为⊙O的切线;(2)、若BP=1,CP= ,求 ⊙O的半径;24. 已知O为直线MN上一点,OP⊥MN,在等腰Rt△ABO中,∠BAO=90°,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.
(1)、求证:CP为⊙O的切线;(2)、若BP=1,CP= ,求 ⊙O的半径;24. 已知O为直线MN上一点,OP⊥MN,在等腰Rt△ABO中,∠BAO=90°,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.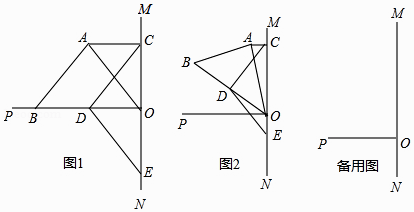 (1)、如图1,若点B在OP上,则
(1)、如图1,若点B在OP上,则①ACOE(填“<”,“=”或“>”);
②线段CA、CO、CD满足的等量关系式是;
(2)、将图1中的等腰Rt△ABO绕O点顺时针旋转α(0°<α<45°),如图2,那么(1)中的结论②是否成立?请说明理由;(3)、将图1中的等腰Rt△ABO绕O点顺时针旋转α(45°<α<90°),请你在图3中画出图形,并直接写出线段CA、CO、CD满足的等量关系式 .25. 两条抛物线 与 的两个交点 、 都在 轴上,抛物线 的顶点为 .(1)、求抛物线 的解析式;(2)、在y轴正半轴上有一点 ,当 时,求 的面积;(3)、判断在 轴上是否存在点 ,使点 绕点 顺时针旋转 ,得到点 恰好落在抛物线 上?若存在,求出点 的坐标;若不存在,请说明理由.