初中数学苏科版九年级上册第二章 圆 单元测试
试卷更新日期:2020-09-28 类型:单元试卷
一、单选题
-
1. 下列判断结论正确的有( )(1)直径是圆中最大的弦. (2)长度相等的两条弧一定是等弧. (3)面积相等的两个圆是等圆. (4)同一条弦所对的两条弧一定是等弧.(5)圆上任意两点间的部分是圆的弦.A、1个 B、2个 C、3个 D、4个2. 在数轴上,点 所表示的实数为 ,点 所表示的实数为 , 的半径为 .那么下列说法中不正确的是( )A、当 时,点 在 外 B、当 时,点 在 内 C、当 时,点 在 内 D、当 时,点 在 外3. 如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
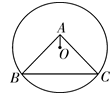 A、2 B、 C、4 D、34. 如图,点A,B,C,D,E在⊙O上, 的度数为60°,则∠B+∠D的度数是( )
A、2 B、 C、4 D、34. 如图,点A,B,C,D,E在⊙O上, 的度数为60°,则∠B+∠D的度数是( ) A、180° B、120° C、100° D、150°5. 如图,在 中,弦 ,点C在 上移动,连接 ,过点C作 交 于点D,则 的最大值是( )
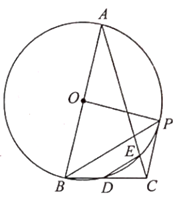
A、180° B、120° C、100° D、150°5. 如图,在 中,弦 ,点C在 上移动,连接 ,过点C作 交 于点D,则 的最大值是( )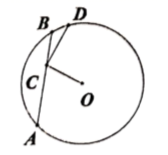 A、2 B、4 C、6 D、86. 如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=70°,∠C=50°,则∠ADB的度数是( )
A、2 B、4 C、6 D、86. 如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=70°,∠C=50°,则∠ADB的度数是( )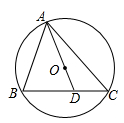 A、70° B、80° C、82° D、85°7. 在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有4个点在圆内,则r的取值范围为( )
A、70° B、80° C、82° D、85°7. 在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有4个点在圆内,则r的取值范围为( ) A、 B、 C、 D、8. 如图,四边形PAOB是扇形OMN的内接矩形,顶点P在 上,且不与M、N重合,当P点在 上移动时,矩形PAOB的形状,大小随之变化,则AB的长度( )
A、 B、 C、 D、8. 如图,四边形PAOB是扇形OMN的内接矩形,顶点P在 上,且不与M、N重合,当P点在 上移动时,矩形PAOB的形状,大小随之变化,则AB的长度( ) A、不变 B、变小 C、变大 D、不能确定9. 如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,距拖拉机中心50米的范围内均会受到噪音影响,已知有两台相距40米的拖拉机正沿ON方向行驶,它们的速度均为10米/秒,则这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间为( )
A、不变 B、变小 C、变大 D、不能确定9. 如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,距拖拉机中心50米的范围内均会受到噪音影响,已知有两台相距40米的拖拉机正沿ON方向行驶,它们的速度均为10米/秒,则这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间为( )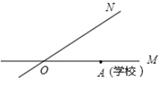 A、6秒 B、8秒 C、10秒 D、18秒10. 已知点 和直线 ,求点P到直线 的距离d可用公式 计算.根据以上材料解决下面问题:如图, 的圆心C的坐标为 ,半径为1,直线l的表达式为 ,P是直线l上的动点,Q是 上的动点,则 的最小值是( )
A、6秒 B、8秒 C、10秒 D、18秒10. 已知点 和直线 ,求点P到直线 的距离d可用公式 计算.根据以上材料解决下面问题:如图, 的圆心C的坐标为 ,半径为1,直线l的表达式为 ,P是直线l上的动点,Q是 上的动点,则 的最小值是( ) A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
11. 若一个圆锥的主视图是一个腰长为6cm,底边长为2cm的等腰三角形,则这个圆锥的侧面积为cm²。12. 已知⊙O的直径长为10,弦AB长为8,弦长CD为6,且AB∥CD,则弦AB与CD之间的距离为.13. 过A,C,D三点的圆的圆心为E,过B,E两点的圆的圆心为D,如果∠A=60°,那么∠B为.
 14. 如图, 的半径 弦 于点 ,连结 并延长交 于点 ,连结 .若 , ,则 的长为 .
14. 如图, 的半径 弦 于点 ,连结 并延长交 于点 ,连结 .若 , ,则 的长为 .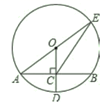 15. 如图,在⊙O中,直径AB与弦CD的交点为E,AC∥OD.若∠BEC=72°,则∠B=°.
15. 如图,在⊙O中,直径AB与弦CD的交点为E,AC∥OD.若∠BEC=72°,则∠B=°.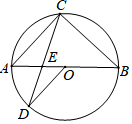 16. 如图,在 中, , , 的内切圆圆 与边 分别相切于点 、 、 ,则 的度数为 .
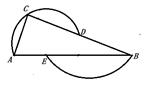
16. 如图,在 中, , , 的内切圆圆 与边 分别相切于点 、 、 ,则 的度数为 .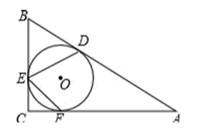 17. 如图,已知AB是半圆的直径,且AB=10,弦AC=6,将半圆沿过点A的直线折叠,使点C落在直径AB上的点C′,则折痕AD的长为 .
17. 如图,已知AB是半圆的直径,且AB=10,弦AC=6,将半圆沿过点A的直线折叠,使点C落在直径AB上的点C′,则折痕AD的长为 .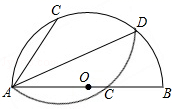 18. 如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=BC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是.
18. 如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=BC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是.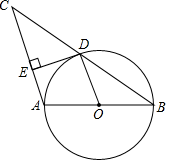 19. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为.
19. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为.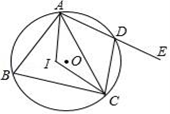 20. 如图,边长为2 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为cm.
20. 如图,边长为2 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为cm. 21. 如图,在△ABC中,AB=10,AC=8,BC=6,以边AB中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是.
21. 如图,在△ABC中,AB=10,AC=8,BC=6,以边AB中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是. 22. 如图,以 为圆心,半径为2的圆与 轴交于 、 两点,与 轴交于 , 两点,点 为圆 上一动点, 于 ,当点 在圆 的运动过程中,线段 的长度的最小值为.
22. 如图,以 为圆心,半径为2的圆与 轴交于 、 两点,与 轴交于 , 两点,点 为圆 上一动点, 于 ,当点 在圆 的运动过程中,线段 的长度的最小值为.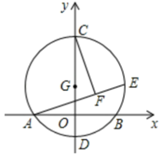
三、解答题
-
23. 已知:如图,△ABC内接于⊙O,AE是⊙O的直径,AD⊥BC 于点D,∠BAE与∠CAD相等吗?若相等,请给出证明;若不相等, 请说明理由
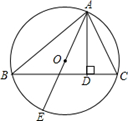 24. △ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是 的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).
24. △ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是 的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).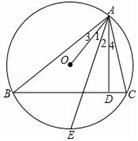 25. 如图,在 中, ,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作 ,交⊙O于点F,求证:
25. 如图,在 中, ,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作 ,交⊙O于点F,求证: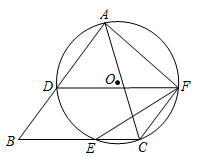 (1)、四边形DBCF是平行四边形(2)、
(1)、四边形DBCF是平行四边形(2)、