初中数学苏科版八年级上册第二章 轴对称图形 单元测试
试卷更新日期:2020-09-27 类型:单元试卷
一、单选题
-
1. 图书馆的标志是浓缩了图书馆文化的符号,下列图书馆标志中,不是轴对称的是( )。A、
 B、
B、 C、
C、 D、
D、 2. 如图, 中, ,点 、 在 、 上,沿 向内折叠 ,得 ,则图中 的和等于( )
2. 如图, 中, ,点 、 在 、 上,沿 向内折叠 ,得 ,则图中 的和等于( )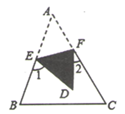 A、 B、 C、 D、3. 点P在∠AOB的平分线上,点P到OA边的距离等于6,点Q是OB边上的任意一点,则下列选项正确的是( )A、
A、 B、 C、 D、3. 点P在∠AOB的平分线上,点P到OA边的距离等于6,点Q是OB边上的任意一点,则下列选项正确的是( )A、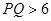 B、
B、 C、
C、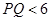 D、
D、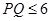 4. 如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
4. 如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )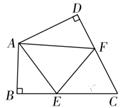 A、50° B、60° C、70° D、80°5. 如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P , DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A、50° B、60° C、70° D、80°5. 如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P , DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( ) A、3 B、4 C、5 D、66. 如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC=24,则△BMN的周长是( )
A、3 B、4 C、5 D、66. 如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC=24,则△BMN的周长是( )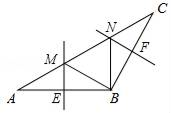 A、36 B、24 C、18 D、167. 已知∠AOB=30°,点P在∠AOB的内部,点P1和点P关于OA对称,点P2和点P关于OB对称,则P1、O、P2三点构成的三角形是( )A、直角三角形 B、钝角三角形 C、等腰直角三角形 D、等边三角形8. 如图,在 中 , ,面积是 , 的垂直平分线 分别交AC,AB边于E,F点,若点 为 边的中点,点 为线段上一动点,则 周长的最小值为( ).
A、36 B、24 C、18 D、167. 已知∠AOB=30°,点P在∠AOB的内部,点P1和点P关于OA对称,点P2和点P关于OB对称,则P1、O、P2三点构成的三角形是( )A、直角三角形 B、钝角三角形 C、等腰直角三角形 D、等边三角形8. 如图,在 中 , ,面积是 , 的垂直平分线 分别交AC,AB边于E,F点,若点 为 边的中点,点 为线段上一动点,则 周长的最小值为( ).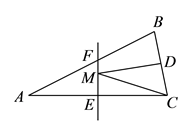 A、 B、 C、 D、9. 如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
A、 B、 C、 D、9. 如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( ) A、①②③ B、①③④ C、①④ D、①②④10. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= AC•BD,其中正确的结论有( )
A、①②③ B、①③④ C、①④ D、①②④10. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= AC•BD,其中正确的结论有( ) A、①② B、①③ C、②③ D、①③②
A、①② B、①③ C、②③ D、①③②二、填空题
-
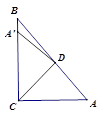
11. 已知等腰三角形的其中两边长为6cm和8cm,则这个三角形的周长为cm.12. 等腰三角形的顶角是50°,则它一腰上的高与底边的夹角为.13. 若等腰三角形一腰上的高与腰长之比为1:2,则该等腰三角形顶角的度数为。14. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A'处,折痕为CD,则∠A'DB=度。
 15. 如图,△ABC的三边AB、BC、CA长分别是40、60、80,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于 .
15. 如图,△ABC的三边AB、BC、CA长分别是40、60、80,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于 .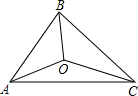 16. 如图,已知钝角三角形ABC的面积为20,最长边AB=10,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为 .
16. 如图,已知钝角三角形ABC的面积为20,最长边AB=10,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为 .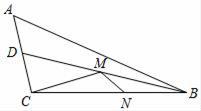 17. 如图,等边 中, , 分别是 、 边上的一点,且 ,则 .
17. 如图,等边 中, , 分别是 、 边上的一点,且 ,则 .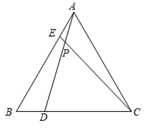 18. 如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为 .
18. 如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为 .
三、综合题
-
19. 作图题(保留作图痕迹,不写画法).(1)、请在坐标系中,画出△ABC关于y轴对称的△A′B′C′.
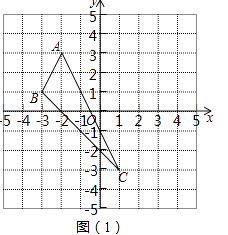 (2)、如图(2),A与B是两个居住社区,OC与OD是两条交汇的公路,欲建立一个超市M,使它到A、B两个社区的距离相等,且到两条公路OC、OD的距离也相等.请利用尺规作图,确定超市M的位置.
(2)、如图(2),A与B是两个居住社区,OC与OD是两条交汇的公路,欲建立一个超市M,使它到A、B两个社区的距离相等,且到两条公路OC、OD的距离也相等.请利用尺规作图,确定超市M的位置.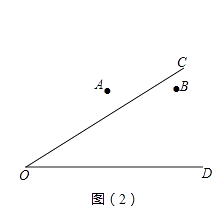 20. 如图,已知点D,E分别是 的边 和 延长线上的点,作 的平分线 ,若 .
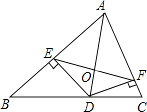
20. 如图,已知点D,E分别是 的边 和 延长线上的点,作 的平分线 ,若 .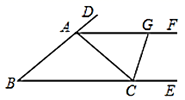 (1)、求证: 是等腰三角形;(2)、作 的平分线交 于点 ,若 ,求 的度数.21. 如图,已知 ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
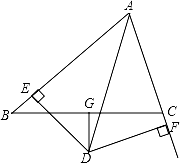
(1)、求证: 是等腰三角形;(2)、作 的平分线交 于点 ,若 ,求 的度数.21. 如图,已知 ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F. (1)、求证:BE=AD;(2)、求∠BFD的度数.22. 如图,在 中,AB边的垂直平分线 交BC于点D,AC边的垂直平分线 交BC于点E, 与 相交于点O,联结OB、OC,若 的周长为6cm, 的周长为16cm.
(1)、求证:BE=AD;(2)、求∠BFD的度数.22. 如图,在 中,AB边的垂直平分线 交BC于点D,AC边的垂直平分线 交BC于点E, 与 相交于点O,联结OB、OC,若 的周长为6cm, 的周长为16cm.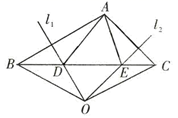 (1)、求线段BC的长;(2)、联结OA,求线段OA的长;(3)、若 ,求 的度数.23. 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)、求线段BC的长;(2)、联结OA,求线段OA的长;(3)、若 ,求 的度数.23. 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F. (1)、求证:OE是CD的垂直平分线.(2)、若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
(1)、求证:OE是CD的垂直平分线.(2)、若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.