山东省枣庄市山亭区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 下列条件中,能判断四边形是菱形的是( )A、对角线互相垂直且相等的四边形 B、对角线互相垂直的四边形 C、对角线相等的平行四边形 D、对角线互相平分且垂直的四边形2. 下列一元二次方程没有实数根的是( )A、x2+x+3=0 B、x2+2x+1=0 C、x2﹣2=0 D、x2﹣2x﹣3=03. 在一个不透明的盒子中,红色、白色、黑色的球共有40个,除颜色外其他完全相同,老师在课堂上组织同学通过多次试验后发现其中摸到红色、白色的频率基本稳定在45%和15%,则盒子中黑色球的个数可能是( ).A、16 B、18 C、20 D、224. 已知2x=3y , 则下列比例式成立的是( )A、 B、 C、 D、5. 用配方法解方程x2﹣2x﹣2=0,原方程应变形为( )A、(x+1)2=3 B、(x﹣1)2=3 C、(x+1)2=1 D、(x﹣1)2=16. 若(a+b﹣1)(a+b+1)﹣4=0,则a+b的值为( )A、2 B、±2 C、 D、±7. 如图,正方形ABCD的边长为1,E为BC上任意一点,EF⊥AC于F,EG⊥BC于G,则EF+EG的值为( )
 A、 B、2 C、3 D、8. 如图,某小区有一长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为( )米.
A、 B、2 C、3 D、8. 如图,某小区有一长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为( )米.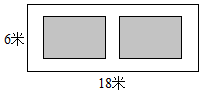 A、2 B、1 C、8或1 D、89. 关于的方程ax2+bx+c=2与方程(x+1)(x-3)=0的解相同,则a-b+c的值等( )A、-2 B、0 C、1 D、210. 若关于 的一元二次方程 有一个根为0,则 的值( )A、0 B、1或2 C、1 D、211. 如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A、2 B、1 C、8或1 D、89. 关于的方程ax2+bx+c=2与方程(x+1)(x-3)=0的解相同,则a-b+c的值等( )A、-2 B、0 C、1 D、210. 若关于 的一元二次方程 有一个根为0,则 的值( )A、0 B、1或2 C、1 D、211. 如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( ) A、 B、 C、 D、12. 如图,已知直线l1∥l2∥l3∥l4 , 相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为( )
A、 B、 C、 D、12. 如图,已知直线l1∥l2∥l3∥l4 , 相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为( )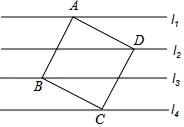 A、 B、 C、3 D、5
A、 B、 C、3 D、5二、填空题
-
13. 已知关于 的方程 有两个不相等的实数根,则 的取值范围是 .14.
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为
 15. 已知 ,则 的值为 .16. 对于任意实数a,b,定义a*b=a(a+b)+b,已知a*4=25,则实数a的值是 .17. 三角形的每条边的长都是方程 的根,则三角形的周长是.18. 在矩形ABCD中,AB=5,AD=12,P是AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF= .
15. 已知 ,则 的值为 .16. 对于任意实数a,b,定义a*b=a(a+b)+b,已知a*4=25,则实数a的值是 .17. 三角形的每条边的长都是方程 的根,则三角形的周长是.18. 在矩形ABCD中,AB=5,AD=12,P是AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF= .
三、解答题
-
19. 解下列方程:(1)、x²-4x+2=0(用配方法);(2)、3x²-7x+3=-1(用公式法).20. 关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1、x2 .(1)、求k的取值范围;(2)、若x1+x2=1﹣x1x2 , 求k的值.21. 某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A篮球;B乒乓球;C羽毛球;D足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
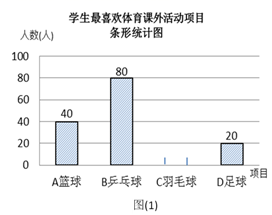
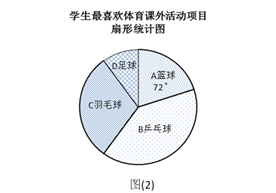 (1)、这次被调查的学生共有人;(2)、请你将条形统计图(1)补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)22. 如图,在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:AF=BE.
(1)、这次被调查的学生共有人;(2)、请你将条形统计图(1)补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)22. 如图,在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:AF=BE. 23. 如图,在 中, ,点 是 中点, , .
23. 如图,在 中, ,点 是 中点, , . (1)、求证:四边形 是菱形;(2)、过点 作 于点 , , ,求 的长.24. 阅读材料:若 ,求m、n的值.
(1)、求证:四边形 是菱形;(2)、过点 作 于点 , , ,求 的长.24. 阅读材料:若 ,求m、n的值.解: ,
,
,
.
根据你的观察,探究下面的问题:
(1)、已知 ,求 的值.(2)、已知△ABC的三边长a、b、c都是正整数,且满足 ,求边c的最大值.(3)、若已知 ,求 的值.25. 如图,A、B、C、D为矩形的4个顶点,AB=16cm , BC=6cm , 动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动. (1)、若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q两点之间的距离是多少cm?(2)、若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?(3)、若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
(1)、若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q两点之间的距离是多少cm?(2)、若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?(3)、若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?