山东省潍坊市青州市2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，不是一元二次方程的是（）

A、 $\frac{1}{x^{2}}$ + $\frac{1}{x}$ ＝1 B、x²＝x+1 C、7x²+3＝0 D、 $\frac{x^{2}}{2}$ ﹣7＝6

查看试题解析
2. 已知α是锐角，sinα=cos60°，则α等于（）

A、30° B、45° C、60° D、不能确定

查看试题解析
3. 用配方法解方程 $x^{2} + 8 x + 9 = 0$ ，变形后的结果正确的是（）

A、 ${(x + 4)}^{2} = - 9$ B、 ${(x + 4)}^{2} = - 7$ C、 ${(x + 4)}^{2} = 25$ D、 ${(x + 4)}^{2} = 7$

查看试题解析
4. 如图所示，A，B，C，D均在正方形网格中的格点上， $∠ B A D ， ∠ C A D$ 分别用 $α$ 和 $β$ 表示，下列四个选项中正确的是（）

A、 $\sin α = \cos α$ B、 $\sin α = \tan α$ C、 $\sin β = \cos β$ D、 $\sin β = \tan β$

查看试题解析
5. 已知在 $⊙ O$ 中，弦AB的长为8，圆心O到AB的距离为3，则 $⊙ O$ 的面积是（）

A、 $9 π$ B、 $16 π$ C、 $25 π$ D、 $64 π$

查看试题解析
6. 如图， $R t △ A B C$ 中， $∠ C = 90^{°}$ ，D为BC上一点， $∠ B = ∠ D A C = 30^{°}$ ， $B D = 2$ ，则AC的长是（）

A、 $\sqrt{3}$ B、 $2 \sqrt{2}$ C、3 D、 $\frac{3}{2} \sqrt{3}$

查看试题解析
7. 如图，PA与⊙O相切于点A，线段PO交⊙O于点C，过点C作⊙O的切线交PA于点B．若PC＝4，AB＝3，则⊙O的半径等于（）

A、4 B、5 C、6 D、12

查看试题解析
8. 若方程 $x^{2} - 7 x + 12 = 0$ 的两个实数根恰好是 $Rt △ A B C$ 的两边的长，则 $△ A B C$ 的周长等于（）

A、12 B、 $7 + \sqrt{7}$ C、12或 $7 + \sqrt{7}$ D、 $8 + 2 \sqrt{10}$ 或 $8 + 4 \sqrt{2}$

查看试题解析
9. 如图，将半径为2，圆心角为90°的扇形BAC绕A点逆时针旋转60°，点B ， C的对应点分别为点D ， E ，则阴影部分的面积为（）

A、 $\sqrt{3} + \frac{π}{3}$ B、 $\sqrt{3} - \frac{π}{3}$ C、 $\frac{π}{3}$ D、π﹣ $\sqrt{3}$

查看试题解析
10. 如图，山上有一座高塔，山脚下有一圆柱形建筑物平台，高塔及山的剖面与圆柱形建筑物平台的剖面ABCD在同一平面上，在点A处测得塔顶H的仰角为35°，在点D处测得塔顶H的仰角为45°，又测得圆柱形建筑物的上底面直径AD为6m，高CD为2.8m，则塔顶端H到地面的高度HG为（）
（参考数据： $\sin 35 ° \approx 0.57$ ， $\cos 35 ° \approx 0.82$ ， $\tan 35 ° \approx 0.70$ ， $\sqrt{2} \approx 1.41$ ）

A、10.8m B、14m C、16.8m D、29.8m

查看试题解析
11. 文艺复兴时期，意大利艺术大师达·芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达·芬奇的“猫眼”，可看成圆与正方形的各边均相切，切点分别为 $A ， B ， C ， D$ ， $\overset{⌢}{B D}$ 所在圆的圆心为点 $A$ （或 $C$ ）. 若正方形的边长为2，则图中阴影部分的面积为（）

A、 $\sqrt{2}$ B、2 C、 $π - 1$ D、 $4 - \frac{π}{2}$

查看试题解析
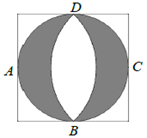12. 若x₁是方程ax²+2x+c＝0(a≠0)的一个根，设M＝(ax₁+1)² ， N＝2﹣ac，则M与N的大小关系为（）

A、M＞N B、M＝N C、M＜N D、不能确定

查看试题解析

二、填空题

13. 如图，某地修建高速公路，要从B地向C地修一座隧道（B，C在同一水平上），某工程师乘坐热气球从B地出发，垂直上升100m到达A处，在A处观测C地的俯角为30°，则B、C两地之间的距离为m.

查看试题解析
14. 已知关于x的一元二次方程 $(m + 2) x^{2} + 4 x - 4 + m^{2} = 0$ 的常数项等于0，则该方程的两根之和等于.

查看试题解析
15. 如图， $A B$ 与 $⊙ O$ 相切于点 $B$ ， $A O$ 的延长线交 $⊙ O$ 于点 $C$ ，连接 $B C$ ，若 $∠ A B C = 120 °$ ， $O C = 3$ ，则劣弧 $B C$ 的长为（结果保留 $π$ ）．

查看试题解析
16. 如图，四边形ABCD内接于 $⊙ O$ ，AB是直径， $O D / / B C ， ∠ A B C = 40^{°}$ ，则 $∠ B C D$ 的度数为.

查看试题解析
17. 如图，一艘轮船在A处测得灯塔P在船的北偏东30°方向，轮船沿着北偏东60°方向航行16km后到达B处，这时灯塔P在船的北偏西75°方向.则灯塔P与B之间的距离等于km（结果保留根号）

查看试题解析
18. 下列一组方程：① $x + \frac{2}{x} = 3$ ，② $x + \frac{6}{x} = 5$ ，③ $x + \frac{12}{x} = 7$ ，…小明通过观察，发现了其中蕴含的规律，并顺利地求出了前三个方程的解第①个方程的解为 $x_{1} = 1 ， x_{2} = 2$ ；第②个方程的解为 $x_{1} = 2 ， x_{2} = 3$ ；第③个方程的解为 $x_{1} = 3 ， x_{2} = 4$ .若n为正整数，且关于x的方程 $x + \frac{n^{2} + n}{x + 3} = 2 n - 2$ 的一个解是 $x = 7$ ，则n的值等于.

查看试题解析

三、解答题

19.

(1)、计算： $\tan 60^{°} + 9 \tan 30^{°} - 8 \sin 60^{°} + 2 \cos 45^{°}$

(2)、在 $△ A B C$ 中， $∠ C = 90^{°}, A C = \sqrt{2}, B C = \sqrt{6}$ ，求 $∠ A$ 的度数

查看试题解析
20. 解下列方程：

(1)、 $x^{2} - 2 x - 15 = 0$

(2)、 ${(x + 1)}^{2} = 4 {(x - 1)}^{2}$

(3)、 $x^{2} - 3 x + 1 = 0$

查看试题解析
21. 已知．在△ABC中，如图，BC= $\sqrt{2}$ AC，∠BCA=135°，求tanA的值．

查看试题解析
22. 如图，AB为 $⊙ O$ 的直径，C、D为 $⊙ O$ 上两点，且 $\overset{⌢}{B C} = \overset{⌢}{C D} ， C F ⊥ A D$ ，垂足为F，直线CF交AB的延长线于点E，连接AC

(1)、判断EF与 $⊙ O$ 的位置关系，并说明理由：

(2)、若 $∠ F E A = 30^{°}$ ， $⊙ O$ 的半径为4，求线段CF的长.

查看试题解析
23. 如图，小明为了测量小河对岸大树BC的高度，他在点A测得大树顶端B的仰角是45°，沿斜坡走 $\frac{3 \sqrt{5}}{2}$ 米到达斜坡上点D ，在此处测得树顶端点B的仰角为31°，且斜坡AF的坡比为1：2（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）．

(1)、求小明从点A走到点D的过程中，他上升的高度；

(2)、大树BC的高度约为多少米？

查看试题解析
24. 已知，如图，AB是 $⊙ O$ 的直径，C是 $⊙ O$ 上一点，连接AC，过点C作直线 $C D ⊥ A B$ 于D（ $A D < D B$ ），点E是DB上任意一点（点D、B除外），直线CE交 $⊙ O$ 于点F.连接AF与直线CD交于点G.

(1)、求证： $A C^{2} = A G \cdot A F$

(2)、若点E是AD（点A除外）上任意一点，上述结论是否仍然成立？若成立，请画出图形并给予证明；若不成立，请说明理由。

查看试题解析