山东省威海市文登区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2米,则这个坡面的坡度为( )A、1:2 B、1:3 C、1: D、:12. 二次函数 ,其对称轴为 ,若 是抛物线上三点,则 的大小关系是( )A、 B、 C、 D、3. 如图,在直角三角形 中, 是斜边 上的中线,已知 则 的值是( )
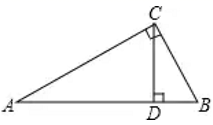 A、 B、 C、 D、4. 已知平面直角坐标系中有两个二次函数 及 的图象,将二次函数 的图象依下列哪一种平移方式后,会使得此两图象对称轴重叠( )A、向左平移4个单位长度 B、向右平移4个单位长度 C、向左平移10个单位长度 D、向右平移10个单位长度5. 王师傅在楼顶上的点 处测得楼前一棵树 的顶端 的俯角为 ,又知水平距离 ,楼高 ,则树高 为( )A、 B、 C、 D、6. 如图,点 在函数 的图象上,且 ,过点 作 轴于点 ,则 的周长为( )
A、 B、 C、 D、4. 已知平面直角坐标系中有两个二次函数 及 的图象,将二次函数 的图象依下列哪一种平移方式后,会使得此两图象对称轴重叠( )A、向左平移4个单位长度 B、向右平移4个单位长度 C、向左平移10个单位长度 D、向右平移10个单位长度5. 王师傅在楼顶上的点 处测得楼前一棵树 的顶端 的俯角为 ,又知水平距离 ,楼高 ,则树高 为( )A、 B、 C、 D、6. 如图,点 在函数 的图象上,且 ,过点 作 轴于点 ,则 的周长为( )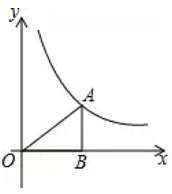 A、 B、 C、 D、7. 某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆.当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A、 B、 C、 D、7. 某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆.当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A、140元 B、150元 C、160元 D、180元8. 如图,点A(a , 1)、B(﹣1,b)都在双曲线y=﹣ 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )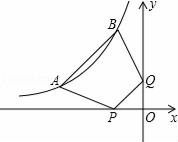 A、y=x B、y=x+1 C、y=x+2 D、y=x+39. 抛物线 上部分点的横坐标 ,纵坐标 的对应值如下表:
A、y=x B、y=x+1 C、y=x+2 D、y=x+39. 抛物线 上部分点的横坐标 ,纵坐标 的对应值如下表:
从上表可知,下列说法中正确的是( ) (填写序号)
①抛物线与 轴的一个交点为 ②函数 的最大值为6③抛物线的对称轴是直线 ,④在对称轴左侧, 随 增大而增大
A、①②③ B、①②④ C、①②③④ D、①③④10. 如图, 为坐标原点,点 在 轴的正半轴上,四边形 是平行四边形, ,反比例函数 在第一象限内的图像经过点 ,与 交于点 ,若点 为 的中点,且 的面积为12,则 的值为( )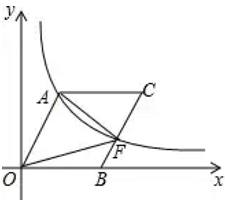 A、16 B、24 C、36 D、4811. 如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2 , y2)是抛物线上任意一点,有下列结论:①二次函数y=ax2+bx+c的最小值为﹣4a;②若﹣1≤x2≤4,则0≤y2≤5a;③若y2>y1 , 则x2>4;④一元二次方程cx2+bx+a=0的两个根为﹣1和 其中正确结论的个数是( )
A、16 B、24 C、36 D、4811. 如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2 , y2)是抛物线上任意一点,有下列结论:①二次函数y=ax2+bx+c的最小值为﹣4a;②若﹣1≤x2≤4,则0≤y2≤5a;③若y2>y1 , 则x2>4;④一元二次方程cx2+bx+a=0的两个根为﹣1和 其中正确结论的个数是( )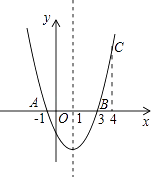 A、1 B、2 C、3 D、412. 如图1中, ,点 从点 出发以 的速度沿折线 运动,点 从点 出发以 的速度沿 运动, 两点同时出发,当某一点运动到点 时,两点同时停止运动.设运动时间为 , 的面积为 ), 关于 的函数图象由 两段组成,如图2所示,有下列结论:① ;② :③图象 段的函数表达式为 ;④ 面积的最大值为8,其中正确的个数有( )个
A、1 B、2 C、3 D、412. 如图1中, ,点 从点 出发以 的速度沿折线 运动,点 从点 出发以 的速度沿 运动, 两点同时出发,当某一点运动到点 时,两点同时停止运动.设运动时间为 , 的面积为 ), 关于 的函数图象由 两段组成,如图2所示,有下列结论:① ;② :③图象 段的函数表达式为 ;④ 面积的最大值为8,其中正确的个数有( )个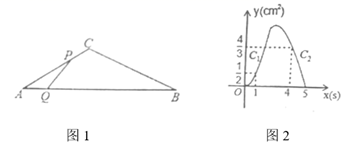 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
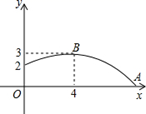
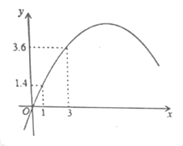
13. 函数 的自变量 的取值范围是 .14. 三角形 中, ,则 值为 .15. 如图,是一学生掷铅球时,铅球行进高度 的函数图象,点 为抛物线的最高点,则该同学的投掷成绩为米.
 16. 如图,在四边形 中, ,连接 , .若 , , ,则 .
16. 如图,在四边形 中, ,连接 , .若 , , ,则 .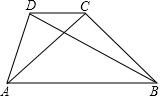 17. 如图,点 ,点 ,…点 在函数 的图象上, 都是等腰直角三角形,斜边 都在 轴上(n是大于或等于2的正数数),则 .(用含 的式子表示)
17. 如图,点 ,点 ,…点 在函数 的图象上, 都是等腰直角三角形,斜边 都在 轴上(n是大于或等于2的正数数),则 .(用含 的式子表示)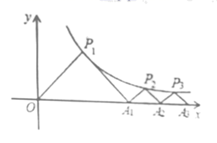 18. 已知二次函数 1的图象过点 则 的最大值为 .
18. 已知二次函数 1的图象过点 则 的最大值为 .三、解答题
-
19.20. 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度.一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60 海里,在B处测得C在北偏东45º的方向上,A处测得C在北偏西30º的方向上,在海岸线AB上有一灯塔D,测得AD=120 海里.
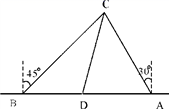 (1)、分别求出A与C及B与C的距离AC,BC(结果保留根号)(2)、已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(1)、分别求出A与C及B与C的距离AC,BC(结果保留根号)(2)、已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?(参考数据: =1.41, =1.73, =2.45)
21. 某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,在一段时间内,销售单价是80元时,销售量是200件,而销售单价每降低1元,就可多售出20件.(1)、写出销售量y件与销售单价x元之间的函数关系式;(2)、写出销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式;(3)、若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,则商场销售该品牌童装获得的最大利润是多少?22. 某公司营销 两种产品,根据市场调研,确定两条信息:信息1:销售 种产品所获利润 (万元)与所销售产品 (吨)之间存在二次函数关系,如图所示
信息2:销售 种产品所获利润 (万元)与销售产品 (吨)之间存在正比例函数关系
根据以上信息,解答下列问题:
 (1)、求二次函数的表达式;(2)、该公司准备购进 两种产品共10吨,请设计一个营销方案使销售 两种产品获得的利润之和最大,最大利润是多少万元?23. 如图1,在 中, ,边 的长为 边 的长为 ,在此三角形内有一个矩形 ;点 分别在 上,设 的长为 ,矩形 的面积为 (单位: )
(1)、求二次函数的表达式;(2)、该公司准备购进 两种产品共10吨,请设计一个营销方案使销售 两种产品获得的利润之和最大,最大利润是多少万元?23. 如图1,在 中, ,边 的长为 边 的长为 ,在此三角形内有一个矩形 ;点 分别在 上,设 的长为 ,矩形 的面积为 (单位: )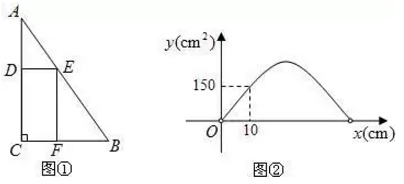 (1)、当 等于30时,求 与 的函数关系式:(不要求写出自变量 的取值范围)(2)、在(1)的条件下,矩形 的面积能否为 ?请说明理由?(3)、若 与 的函数图象如图2所示,求此时 的值24. 如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)、当 等于30时,求 与 的函数关系式:(不要求写出自变量 的取值范围)(2)、在(1)的条件下,矩形 的面积能否为 ?请说明理由?(3)、若 与 的函数图象如图2所示,求此时 的值24. 如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.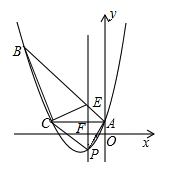 (1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.25. 如图1,抛物线 与 轴交于点 ,与y轴交于点 ,在 轴上有一动点 ,过点E作x轴的垂线交直线 于点N,交抛物线于点P,过点P作 于点M.
(1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.25. 如图1,抛物线 与 轴交于点 ,与y轴交于点 ,在 轴上有一动点 ,过点E作x轴的垂线交直线 于点N,交抛物线于点P,过点P作 于点M.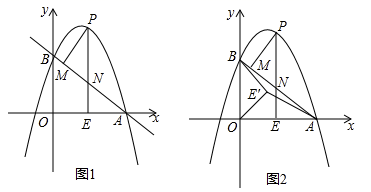 (1)、求a的值和直线 的函数表达式;(2)、设 的周长为 , 的周长为 ,若 ,求m的值;(3)、如图2,在(2)条件下,将线段 绕点O逆时针旋转得到 ,旋转角为 ,连接 、 ,求 的最小值.
(1)、求a的值和直线 的函数表达式;(2)、设 的周长为 , 的周长为 ,若 ,求m的值;(3)、如图2,在(2)条件下,将线段 绕点O逆时针旋转得到 ,旋转角为 ,连接 、 ,求 的最小值.