湖北省武汉市三校2021届九年级上学期数学第一次月考试卷
试卷更新日期:2020-09-27 类型:月考试卷
一、选择题
-
1. 对于函数 ,下列结论错误的是( )A、图象顶点是(2,5) B、图象开口向上 C、图象关于直线 对称 D、函数最大值为52. 已知关于x的一元二次方程x2+bx﹣1=0,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关3. 用配方法解方程 ,配方后的方程是 ( )A、 B、 C、 D、4. 在平面直角坐标系中,将抛物线y=x2﹣2x﹣1先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式是( )A、y=(x+1)2+1 B、y=(x﹣3)2+1 C、y=(x﹣3)2﹣5 D、y=(x+1)2+25. 已知关于 的一元二次方程 有两个不相等的实数根,则k的值可以是( )A、-2 B、1 C、2 D、36. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )A、 B、4 C、﹣ D、﹣7. 某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是 ,则这种植物每个支干长出的小分支个数是( )A、 B、 C、 D、8. 我县某贫围户2016年的家庭年收入为4000元,由于党的扶贫政策的落实,2017、2018年家庭年收入增加到共15000元,设平均每年的增长率为x,可得方程( )A、4000(1+x)2=15000 B、4000+4000(1+x)+4000(1+x)2=15000 C、4000(1+x)+4000(1+x)2=15000 D、4000+4000(1+x)2=150009. 如图,在四边形 中, , , , , .动点M,N同时从点A出发,点M以 的速度沿 向终点B运动,点N以 的速度沿折线 向终点C运动.设点N的运动时间为 , 的面积为 ,则下列图象能大致反映S与t之间函数关系的是( )
 A、
A、 B、
B、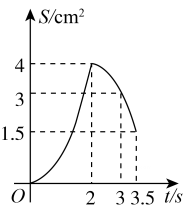 C、
C、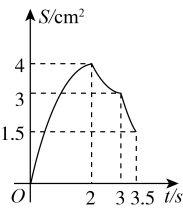 D、
D、 10. 如图,抛物线 与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 ,则下列结论中:① ;② ;③ 与 是抛物线上两点,若 ,则 ;④若抛物线的对称轴是直线 ,m为任意实数,则 ;⑤若 ,则 ,正确的个数是( )
10. 如图,抛物线 与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 ,则下列结论中:① ;② ;③ 与 是抛物线上两点,若 ,则 ;④若抛物线的对称轴是直线 ,m为任意实数,则 ;⑤若 ,则 ,正确的个数是( )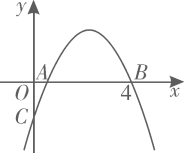 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
11. 方程 的两根为 、 则 的值为.12. 方程 的根是.13. 下表中y与x的数据满足我们初中学过的某种函数关系,其函数表达式为 .
……
-1
0
1
3
……
……
0
3
4
0
……
14. 汽车刹车后行驶的距离s与行驶时间t(秒)的函数关系是s=15t﹣6t2 , 汽车从刹车到停下来所用时间是秒.15. 一个三角形的两边长分别为2和5,第三边长是方程 的根,则该三角形的周长为.16. 二次函数y=ax2+bx+c的图象如图所示,下列结论:①ab>0;②a+b﹣1=0;③a>1;④关于x的一元二次方程ax2+bx+c=0的一个根为1,另一个根为﹣ .其中正确结论的序号是 .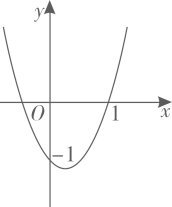
三、解答题
-
17. 解答下列各题:(1)、用配方法解方程: .(2)、已知一元二次方程 的一个根是 .求 的值和方程的另一个根.18. 已知抛物线 .(1)、若抛物线的对称轴为 轴,求 的值;(2)、若抛物线的顶点在 正半轴上,求顶点坐标.19. 如图,抛物线 与x轴交于 两点(点A位于点B的左侧),与y轴的负半轴交于点C.
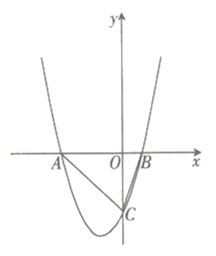 (1)、求点B的坐标.(2)、若 的面积为6.
(1)、求点B的坐标.(2)、若 的面积为6.①求这条抛物线相应的函数解析式.
②在拋物线上是否存在一点P使得 ?若存在,请求出点P的坐标;若不存在,请说明理由.
20. “武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了 条口罩生产线,每条生产线每天可生产口罩 个.如果每增加一条生产线,每条生产线就会比原来少生产 个口罩.设增加 条生产线后,每条生产线每天可生产口罩 个.(1)、直接写出 与 之间的函数关系式;(2)、若每天共生产口罩 个,在投入人力物力尽可能少的情况下,应该增加几条生产线?(3)、设该厂每天可以生产的口罩 个,请求出 与 的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?21. 已知△ABC的两边AB、AC的长恰好是关于x的方程x2+(2k+3)x+k2+3k+2=0的两个实数根,第三边BC的长为5(1)、求证:AB≠AC(2)、如果△ABC是以BC为斜边的直角三角形,求k的值(3)、填空:当k=时,△ABC是等腰三角形,△ABC的周长为22. 在一次聚会上,规定每两个人见面必须握手,且握手1次.(1)、若参加聚会的人数为3,则共握手次;若参加聚会的人数为5,则共握手次;(2)、若参加聚会的人数为n(n为正整数),则共握手次;(3)、若参加聚会的人共握手28次,请求出参加聚会的人数.(4)、嘉嘉由握手问题想到了一个数学问题:若线段AB上共有m个点(不含端点A , B),线段总数为多少呢?请直接写出结论.23. 如图,二次函数 的图象过 、 、 三点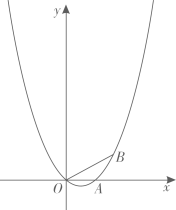 (1)、求二次函数的解析式;(2)、若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;(3)、在直线CD下方的二次函数的图象上有一动点P,过点P作 轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.24. 二次函数 的图象与x轴交于A(2,0),B(6,0)两点,与y轴交于点C,顶点为E.
(1)、求二次函数的解析式;(2)、若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;(3)、在直线CD下方的二次函数的图象上有一动点P,过点P作 轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.24. 二次函数 的图象与x轴交于A(2,0),B(6,0)两点,与y轴交于点C,顶点为E.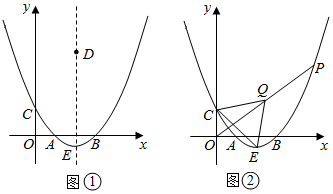 (1)、求这个二次函数的表达式,并写出点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.
(1)、求这个二次函数的表达式,并写出点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.