湖北省黄石市经济开发区2021届九年级上学期数学摸底试卷
试卷更新日期:2020-09-27 类型:开学考试
一、选择题
-
1. 计算 的结果是( )A、±2 B、2 C、-2 D、42. 若二次根式 有意义,则a的取值范围是( )A、a>3 B、a≥3 C、a≤3 D、a≠33. 下列函数中,表示y是x的正比例函数的是( )A、y=﹣0.1x B、y=2x2 C、y2=4x D、y=2x+14. 如果四边形ABCD是平行四边形,AB=6,且AB的长是四边形ABCD周长的 ,那么BC的长是( )A、6 B、8 C、10 D、165. 若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )A、60° B、90° C、120° D、45°6. 为了解某种电动汽车一次充电后行驶的里程数,抽检了10辆车,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是( )
 A、220,220 B、220,210 C、200,220 D、230,2107. 某学校在开展“节约每一滴水”的活动中,从七年级的100名同学中选出20名同学汇报了各自家庭一个月的节水情况,将有关数据(每人上报节水量都是正整数)整理如下表:
A、220,220 B、220,210 C、200,220 D、230,2107. 某学校在开展“节约每一滴水”的活动中,从七年级的100名同学中选出20名同学汇报了各自家庭一个月的节水情况,将有关数据(每人上报节水量都是正整数)整理如下表:节水量x/t
0.5≤x<1.5
1.5≤x<2.5
2.5≤x<3.5
3.5≤x<4.5
人数
6
4
8
2
请你估计这100名同学的家庭一个月节约用水的总量大约是( )
A、180t B、300t C、230t D、250t8. 甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )A、北偏西30° B、南偏西30° C、南偏东60° D、南偏西60°9. 如图,在锐角三角形ABC中,AB= ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )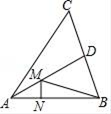 A、4 B、5 C、6 D、1010. 如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组 的解集是( )
A、4 B、5 C、6 D、1010. 如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组 的解集是( )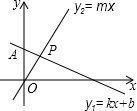 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:2 ﹣6 = .12. 一组数据:25,29,20,x,14,它的中位数是24,则这组数据的平均数为 .13. 如图,从电线杆离地面12m处向地面拉一条长为13m的钢缆,则地面钢缆固定点A到电线杆底部B的距离为 .
 14. 如图,在矩形ABCD中,E是AB边上的中点,将△BCE沿CE翻折得到△FCE,连接AF.若∠EAF=75°,那么∠BCF的度数为 .
14. 如图,在矩形ABCD中,E是AB边上的中点,将△BCE沿CE翻折得到△FCE,连接AF.若∠EAF=75°,那么∠BCF的度数为 . 15. 已知直角三角形的两边长分别为3、4.则第三边长为.16. 如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为 .
15. 已知直角三角形的两边长分别为3、4.则第三边长为.16. 如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为 .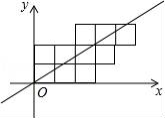
三、解答题
-
17. 计算: 518. 先化简,再求值: ,其中a= +1.19. 已知一次函数的图象过点(3,5)与点(﹣4,﹣9),求这个一次函数的解析式.20. 如图,在四边形ABCD中,AB=CD , BF=DE , AE⊥BD , CF⊥BD , 垂足分别为E、F .
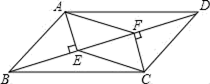 (1)、求证:△ABE≌△CDF;(2)、若AC与BD交于点O , 求证:AO=CO .21. 某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
(1)、求证:△ABE≌△CDF;(2)、若AC与BD交于点O , 求证:AO=CO .21. 某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题: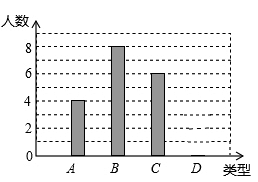
(1)、补全条形图;
(2)、写出这20名学生每人植树量的众数和中位数;(3)、估计这240名学生共植树多少棵?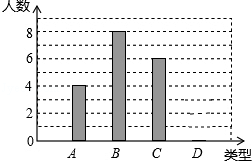 22. 如图,在平面直角坐标系xOy中,直线y=-- x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
22. 如图,在平面直角坐标系xOy中,直线y=-- x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)、求AB的长和点C的坐标;(2)、求直线CD的表达式.
23. 某经销商从市场得知如下信息:A品牌手表
B品牌手表
进价(元/块)
700
100
售价(元/块)
900
160
他计划用4万元资金一次性购进这两种品牌手表共100块,设该经销商购进A品牌手表x块,这两种品牌手表全部销售完后获得利润为y元.
(1)、试写出y与x之间的函数关系式;(2)、若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案?(3)、选择哪种进货方案,该经销商可获利最大?最大利润是多少元?24. 如图,正方形 ABCD 中,P 为 AB 边上任意一点, AE⊥DP 于 E,点 F 在 DP 的延长线 上,且 EF=DE,连接 AF、BF,∠BAF 的平分线交 DF 于 G,连接 GC.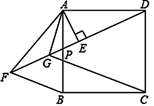 (1)、求证:∠PAE=∠AFD(2)、求证: 是等腰直角三角形(3)、求证:AG+CG = DG.25. 已知:如图1,在平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)、求证:∠PAE=∠AFD(2)、求证: 是等腰直角三角形(3)、求证:AG+CG = DG.25. 已知:如图1,在平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点. (1)、求证:BD∥AC;(2)、若点C在x轴的正半轴上,且BD与AC的距离等于1,求点C的坐标;(3)、如图2,如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
(1)、求证:BD∥AC;(2)、若点C在x轴的正半轴上,且BD与AC的距离等于1,求点C的坐标;(3)、如图2,如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.