辽宁省沈阳市沈北新区2019-2020学年七年级上学期数学期中考试试卷
试卷更新日期:2020-09-27 类型:期中考试
一、选择题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 下面几个几何体,从正面看到的形状是圆的是( )A、
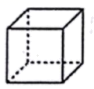 B、
B、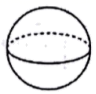 C、
C、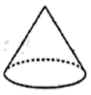 D、
D、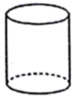 3. 2019沈北蒲河国际马拉松赛于10月13日在蒲河生态廊道和平公园前鸣枪开跑。据了解,本次比赛吸引了4000余名来自全国各地的选手参加。将数据4000用科学记数法表示为( )A、 0.4×103 B、4×104 C、0.4×104 D、4×1034. 某地一天早晨的温度是-7℃,中午上升了15℃,则中午的温度是( )A、-5℃ B、-23℃ C、15℃ D、8℃5. 用代数式表示“a的2倍与3的和”为( )A、2a+3 B、2(a+3) C、3a+2 D、3(a+2)6. 若 与 是同类项,则m,n的值分别为( )A、2,1 B、2,2 C、1,2 D、-2,17.
3. 2019沈北蒲河国际马拉松赛于10月13日在蒲河生态廊道和平公园前鸣枪开跑。据了解,本次比赛吸引了4000余名来自全国各地的选手参加。将数据4000用科学记数法表示为( )A、 0.4×103 B、4×104 C、0.4×104 D、4×1034. 某地一天早晨的温度是-7℃,中午上升了15℃,则中午的温度是( )A、-5℃ B、-23℃ C、15℃ D、8℃5. 用代数式表示“a的2倍与3的和”为( )A、2a+3 B、2(a+3) C、3a+2 D、3(a+2)6. 若 与 是同类项,则m,n的值分别为( )A、2,1 B、2,2 C、1,2 D、-2,17.如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 8. 下列说法:① 一定是负数;:② 一定是正数;③倒数等于它本身的数是±1;④绝对值等于它本身的数是1;其中正确的个数是( )A、1个 B、2个 C、3个 D、4个9. 岩 ,则 的值是( )A、3 B、-1 C、2 D、-210. 如图,某广场地面的图案是用大小相同的黑、白正方形地砖镶嵌而成,图中第1个黑色L形由3个正方形组成,第2个黑色L形由7个正方形组成……那么第n个黑色L形的正方形个数是( )
8. 下列说法:① 一定是负数;:② 一定是正数;③倒数等于它本身的数是±1;④绝对值等于它本身的数是1;其中正确的个数是( )A、1个 B、2个 C、3个 D、4个9. 岩 ,则 的值是( )A、3 B、-1 C、2 D、-210. 如图,某广场地面的图案是用大小相同的黑、白正方形地砖镶嵌而成,图中第1个黑色L形由3个正方形组成,第2个黑色L形由7个正方形组成……那么第n个黑色L形的正方形个数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 硬币在桌面上快速地转动时,看上去象球,这说明了 .
12. 五棱柱有个面,个顶点,条棱.13. 比较大小: .14. 在数轴上,与表示2.5的点距离为3.5的点表示的数是.15. 规定一种新运算: , 如 , 则(-2)△5=16. 若 , ,且 ,那么 .三、解答题
-
17. 把下列各数填入相应的集合中:
,0,7,-0.08,-53,3.14,+22, .
正整数集合:{ …}
分数集合:{ …}
负有理数集合:{ …}
18. 从正面、左面观察如图所示几何体,分别画出你所看到的几何体的形状图.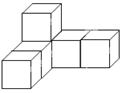 19. 计算(1)、(-10)-28-(-19)+(-21)(2)、(3)、(4)、(5)、(6)、20. 化简下列各式:(1)、(2)、21. 先化简,在求值.(1)、 ,其中 , .(2)、 ,其中 , .22. 某工厂在上一星期的星期日生产了100台彩电,下表是本星期的生产情况:
19. 计算(1)、(-10)-28-(-19)+(-21)(2)、(3)、(4)、(5)、(6)、20. 化简下列各式:(1)、(2)、21. 先化简,在求值.(1)、 ,其中 , .(2)、 ,其中 , .22. 某工厂在上一星期的星期日生产了100台彩电,下表是本星期的生产情况:星期
一
二
三
四
五
六
日
增减/辆
-1
+3
-2
+4
+7
-5
-10
比前一天产量多的计为正数,比前一天产量少的记为负数.请求出本星期的总产量.
23. 已知式 是关于m的多项式,且不含一次项,求k的值.24. 已知 , 互为相反数, , 互为倒数,且 .求代数式 的值.25. 十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列儿种简单多面体模型,解答下列问题: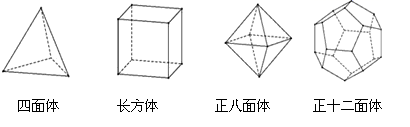 (1)、根据上面多面体模型,完成表格中的空格:
(1)、根据上面多面体模型,完成表格中的空格:多面体
顶点数(V)
面数(F)
棱数(F)
四面体
长方体
正八面体
正十二面体
你发现顶点数(V)、面数(F)、棱数(F)之间存在的关系式是_▲__.
(2)、一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是;(3)、某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.