山东省临沂市兰山区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 近几年我国国产汽车行业蓬勃发展,下列汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图, 为 的直径, 为 上两点,若 ,则 的大小为( ).
2. 如图, 为 的直径, 为 上两点,若 ,则 的大小为( ).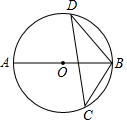 A、60° B、50° C、40° D、20°3. 我省加快新旧动能转换,促进企业创新发展.某企业一月份的营业额是1000万元,月平均增长率相同,今年第一季度的总营业额是3640万元.若设月平均增长率是 ,那么可列出的方程是( )A、 B、 C、 D、4. 将抛物线 向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )A、 B、 C、 D、5. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形AECF的面积为20,DE=2,则AE的长为( )
A、60° B、50° C、40° D、20°3. 我省加快新旧动能转换,促进企业创新发展.某企业一月份的营业额是1000万元,月平均增长率相同,今年第一季度的总营业额是3640万元.若设月平均增长率是 ,那么可列出的方程是( )A、 B、 C、 D、4. 将抛物线 向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )A、 B、 C、 D、5. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形AECF的面积为20,DE=2,则AE的长为( )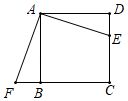 A、4 B、 C、6 D、6. 如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2 , 求道路的宽. 如果设小路宽为x,根据题意,所列方程正确的是( )
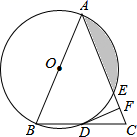
A、4 B、 C、6 D、6. 如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2 , 求道路的宽. 如果设小路宽为x,根据题意,所列方程正确的是( )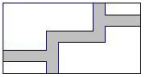 A、(32+x)(20+x)=540 B、(32﹣x)(20﹣x)=540 C、(32+x)(20﹣x)=540 D、(32﹣x)(20+x)=547. 如图,线段 AB 经过⊙O 的圆心, AC , BD 分别与⊙O 相切于点 C ,D .若 AC =BD = 4 ,∠A=45°,则弧CD的长度为( )
A、(32+x)(20+x)=540 B、(32﹣x)(20﹣x)=540 C、(32+x)(20﹣x)=540 D、(32﹣x)(20+x)=547. 如图,线段 AB 经过⊙O 的圆心, AC , BD 分别与⊙O 相切于点 C ,D .若 AC =BD = 4 ,∠A=45°,则弧CD的长度为( )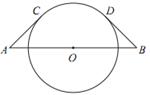 A、π B、2π C、2 π D、4π8. 已知二次函数 的 与 的部分对应值如表:
A、π B、2π C、2 π D、4π8. 已知二次函数 的 与 的部分对应值如表:-1
0
2
3
4
5
0
-4
-3
0
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线: ;③当 时, ;④若 是抛物线上两点,则 ,其中正确的个数是( )
A、0 B、1 C、2 D、39. 如图,分别以等边三角形ABC的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若AB=2,则莱洛三角形的面积(即阴影部分面积)为( )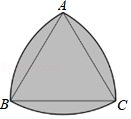 A、 B、 C、2 D、210. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )
A、 B、 C、2 D、210. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )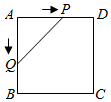 A、
A、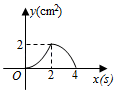 B、
B、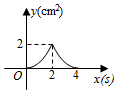 C、
C、 D、
D、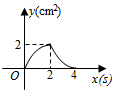
二、填空题
-
11. 如图,在正方形网格中,格点 绕某点顺时针旋转角 得到格点 ,点 与点 ,点 与点 ,点 与点 是对应点,则 度.
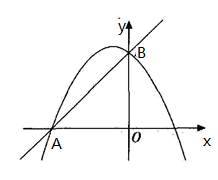
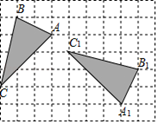 12. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 .
12. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 . 13. 已知关于 的方程 有两个不相等的实数根,则 的取值范围是 .14. 在 中, , ,它的内切圆半径为 ,则 的周长为15. 如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度增加了米.
13. 已知关于 的方程 有两个不相等的实数根,则 的取值范围是 .14. 在 中, , ,它的内切圆半径为 ,则 的周长为15. 如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度增加了米.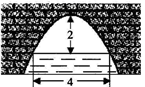 16. 如图, 是 的弦, ,点 是 上的一个动点,且 ,若点 , 分别是 , 的中点,则 的最大值是 .
16. 如图, 是 的弦, ,点 是 上的一个动点,且 ,若点 , 分别是 , 的中点,则 的最大值是 .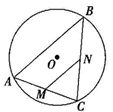
三、解答题
-
17. 用适当的方法解方程.(1)、 ;(2)、 .18.
方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
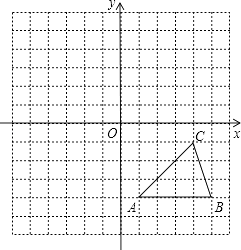 (1)、试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;(2)、以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标.19. 如图, 的平分线交 的外接圆于点 , 的平分线交 于点 .
(1)、试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;(2)、以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标.19. 如图, 的平分线交 的外接圆于点 , 的平分线交 于点 .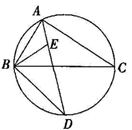 (1)、求证: ;(2)、若 , ,求 外接圆的半径.20. 某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出.已知生产x只玩具熊猫的成本为R(元),售价每只为P(元),且R、P与x的关系式分别为R=500+30x,P=170-2x.(1)、当日产量为多少时,每日获得的利润为1750元?(2)、当日产量为多少时,可获得最大利润?最大利润是多少?
(1)、求证: ;(2)、若 , ,求 外接圆的半径.20. 某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出.已知生产x只玩具熊猫的成本为R(元),售价每只为P(元),且R、P与x的关系式分别为R=500+30x,P=170-2x.(1)、当日产量为多少时,每日获得的利润为1750元?(2)、当日产量为多少时,可获得最大利润?最大利润是多少?