山东省临沂市兰陵县2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1.
下列美丽的图案中，既是轴对称图形又是中心对称图形的个数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 关于 $x$ 的方程 $2 x^{2} - 4 = 0$ 解为（）

A、2 B、±2 C、 $\sqrt{2}$ D、 $\pm \sqrt{2}$

查看试题解析
3. 在平面直角坐标系中，P（﹣1，3）关于原点的对称点Q的坐标是（）

A、（1，3） B、（﹣1，3） C、（1，﹣3） D、（﹣1，﹣3）

查看试题解析
4. 抛物线 $y = \frac{1}{2} {(x - 2)}^{2} - 3$ 的顶点坐标是（）

A、 $(2, - 3)$ B、 $(2, 3)$ C、 $(- 2, 3)$ D、 $(- 2, - 3)$

查看试题解析
5. 若m、n是一元二次方程x²-5x-2=0的两个实数根，则m+n-mn的值是（）

A、-7 B、7 C、3 D、-3

查看试题解析
6. 如图，⊙O的直径为10，AB为弦，OC⊥AB ，垂足为C ，若OC＝3，则弦AB的长为（）

A、8 B、6 C、4 D、10

查看试题解析
7. 如图，AB是⊙O的直径，CD是⊙O的弦，∠ABD＝59°，则∠C等于（）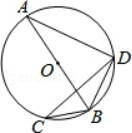

A、29° B、31° C、59° D、62°

查看试题解析
8. 在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M₁N₁P₁ ，则其旋转中心可能是（）

A、点A B、点B C、点C D、点D

查看试题解析
9. 如图，AB是⊙O的直径，弦CD⊥AB ， ∠CDB＝30°，CD＝6，阴影部分图形的面积为（）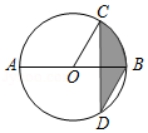

A、4π B、3π C、2π D、π

查看试题解析
10. 已知一元二次方程1–（x–3）（x+2）=0，有两个实数根x₁和x₂（x₁<x₂），则下列判断正确的是（）

A、–2<x₁<x₂<3 B、x₁<–2<3<x₂ C、–2<x₁<3<x₂ D、x₁<–2<x₂<3

查看试题解析
11. 设A(﹣2，y₁)，B(1，y₂)，C(2，y₃)是抛物线 $y = - {(x + 1)}^{2} + 2$ 上的三点，则y₁ ， y₂ ， y₃的大小关系为（）

A、y₁＞y₂＞y₃ B、y₁＞y₃＞y₂ C、y₃＞y₂＞y₁ D、y₃＞y₁＞y₂

查看试题解析
12. 如图，二次函数y=ax²+bx+c（a≠0）的图象与x轴交于点A、B两点，与y轴交于点C，对称轴为直线x=-1，点B的坐标为（1，0），则下列结论：①AB=4；②b²-4ac＞0；③ab＜0；④a²-ab+ac＜0，其中正确的结论有（）个．

A、3 B、4 C、2 D、1

查看试题解析

二、填空题

13. 二次函数 $y = - x^{2} - 2 x + 3$ 的最大值是．

查看试题解析
14. 已知抛物线 $y = x^{2} - (k - 1) x - 3 k - 2$ 与 $x$ 轴交于两点A（ $α$ ，0），B（ $β$ ，0），且 $α^{2} + β^{2} = 17$ ，则 $k$ ＝．

查看试题解析
15. 若二次函数y=x²+2m﹣1的图象经过原点，则m的值是．

查看试题解析
16. 若二次函数 $y = k x^{2} + x + 1$ 的函数值恒为正数，则 $k$ 的取值范围是．

查看试题解析
17. 如图， $∠ M O N = 90 °$ ，矩形 $A B C D$ 的顶点 $A$ 、 $B$ 分别在边 $O M$ 、 $O N$ 上，当 $B$ 在边 $O N$ 上运动时， $A$ 随之在 $O M$ 上运动，矩形 $A B C D$ 的形状保持不变，其中 $A B = 6$ ， $B C = 3$ ，运动过程中，点 $D$ 到点 $O$ 的最大距离为．

查看试题解析
18. 如图，在平面直角坐标系中，将 $△ A B O$ 绕点 $A$ 顺时针旋转到 $△ A_{1} B_{1} C_{1}$ 的位置，点 $B$ 、 $O$ 分别落在点 $B_{1}$ 、 $C_{1}$ 处，点 $B_{1}$ 在 $x$ 轴上，再将 $△ A B_{1} C_{1}$ 绕点 $B_{1}$ 顺时针旋转到 $△ A_{1} B_{1} C_{2}$ 的位置，点 $C_{2}$ 在 $x$ 轴上，将 $△ A_{1} B_{1} C_{2}$ 绕点 $C_{2}$ 顺时针旋转到 $△ A_{2} B_{2} C_{2}$ 的位置，点 $A_{2}$ 在 $x$ 轴上，依次（无滑动）进行下去……．若点 $A (\frac{5}{3} ， 0)$ 、 $B (0 ， 4)$ ，则点 $B_{2018}$ 的坐标为．

查看试题解析

三、解答题

19. 按要求解一元二次方程：

(1)、2x²﹣3x+1=0（配方法）

(2)、x（x﹣2）+x﹣2=0（因式分解法）

查看试题解析
20. 如图，已知：BC与CD重合，∠ABC＝∠CDE＝90°，△ABC≌△CDE，并且△CDE可由△ABC逆时针旋转而得到．请你利用尺规作出旋转中心O(保留作图痕迹，不写作法)，并直接写出旋转角度是．

查看试题解析
21. 某公司今年1月份的生产成本是400万元，由于改进技术，生产成本逐月下降，3月份的生产成本是361万元．假设该公司2、3、4月每个月生产成本的下降率都相同．

(1)、求每个月生产成本的下降率；

(2)、请你预测4月份该公司的生产成本．

查看试题解析
22. 某景区商店销售一种纪念品，每件的进货价为40元．经市场调研，当该纪念品每件的销售价为50元时，每天可销售200件；当每件的销售价每增加1元，每天的销售数量将减少10件．

(1)、当每件的销售价为52元时，该纪念品每天的销售数量为件；

(2)、当每件的销售价x为多少时，销售该纪念品每天获得的利润y最大？并求出最大利润．

查看试题解析
23. 如图， $⊙ O$ 的直径 $A B$ 为 $10 c m$ ，弦 $A C$ 为 $6 c m$ ， $∠ A C B$ 的平分线交 $⊙ O$ 于点 $D$ ，求 $B C$ ， $A D$ ， $B D$ 的长．

查看试题解析
24. 已知：如图，在△ABC中， $A B = A C$ ，以 $A C$ 为直径的⊙O与 $B C$ 交于点 $D$ ， $D E ⊥ A B$ ，垂足为 $E$ ， $E D$ 的延长线与 $A C$ 的延长线交于点 $F$ ．

(1)、求证： $D E$ 是⊙O的切线.

(2)、若⊙O的半径为4， $∠ F = 30 °$ ，求 $D E$ 的长．

查看试题解析
25. 如图，一次函数y=x+m图象过点A(1，0)，交y轴于点 $B$ ， $C$ 为y轴负半轴上一点，且 $B C = 2 O B$ ，过 $A$ 、 $C$ 两点的抛物线交直线 $A B$ 于点 $D$ ，且CD//x轴．

(1)、求这条抛物线的解析式；

(2)、观察图象，写出使一次函数值小于二次函数值时 $x$ 的取值范围；

(3)、在题中的抛物线上是否存在一点 $M$ ，使得 $∠ A D M$ 为直角？若存在，求出点 $M$ 的坐标；若不存在，请说明理由．

查看试题解析