山东省聊城市莘县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
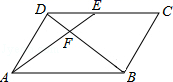
1. 的算术平方根等于( )A、 B、 C、 D、2. 如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F, ,则DE:EC=( )
 A、2:5 B、2:3 C、3:5 D、3:23. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上。若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )
A、2:5 B、2:3 C、3:5 D、3:23. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上。若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )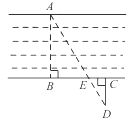 A、60m B、40m C、30m D、20m4. 将三角形纸片 按如图所示的方式折叠,使点 落在边 上,记为点 ,折痕为 .已知 ,若以点 为顶点的三角形与 相似,那么 的长度是( )
A、60m B、40m C、30m D、20m4. 将三角形纸片 按如图所示的方式折叠,使点 落在边 上,记为点 ,折痕为 .已知 ,若以点 为顶点的三角形与 相似,那么 的长度是( )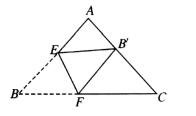 A、 B、 C、 或4 D、 或45. 在△ABC中,∠C=90°,如果tanA= ,那么sinB的值的等于( )A、 B、 C、 D、6. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A、 B、 C、 或4 D、 或45. 在△ABC中,∠C=90°,如果tanA= ,那么sinB的值的等于( )A、 B、 C、 D、6. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )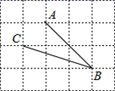 A、 B、2 C、 D、7. 如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m , 点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是( )
A、 B、2 C、 D、7. 如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m , 点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是( )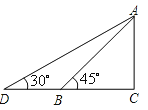 A、2 B、 C、 D、8. 河堤横断面如图所示,迎水坡 米,迎水坡 的坡比为 (坡比是坡面的铅直高度 与水平度 之比),则 的长是( )
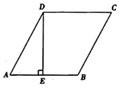
A、2 B、 C、 D、8. 河堤横断面如图所示,迎水坡 米,迎水坡 的坡比为 (坡比是坡面的铅直高度 与水平度 之比),则 的长是( )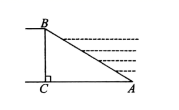 A、 米 B、 米 C、15米 D、10米9. 如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是( )
A、 米 B、 米 C、15米 D、10米9. 如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是( )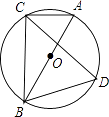 A、30° B、45° C、60° D、75°10. 如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
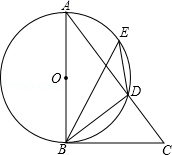
A、30° B、45° C、60° D、75°10. 如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )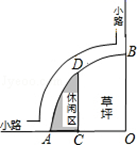 A、 米2 B、 米2 C、 米2 D、 米211. 如图,在同圆中,弧 等于弧 的 倍,试判断 与 的大小关系是( )
A、 米2 B、 米2 C、 米2 D、 米211. 如图,在同圆中,弧 等于弧 的 倍,试判断 与 的大小关系是( )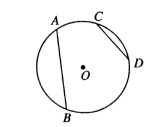 A、 B、 C、 D、不能确定12. 如图,在 中, ,点 是边 上一点,以点 为圆心,以 为半径作圆, 恰好与 相切于点 ,连接 .若 平分 ,则线段 的长是( )
A、 B、 C、 D、不能确定12. 如图,在 中, ,点 是边 上一点,以点 为圆心,以 为半径作圆, 恰好与 相切于点 ,连接 .若 平分 ,则线段 的长是( )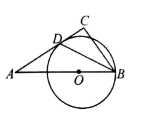 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
13. 在△ABC中,若|cosA- |+(1-tanB)2=0,则∠C的度数是.
14. 已知 中, , ,点 是线段 的中点,点 在线段 上且 ,则 .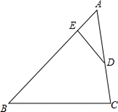 15. 如图, 中, , , ,则 的面积是 .
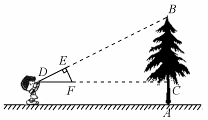
15. 如图, 中, , , ,则 的面积是 .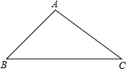 16. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的
16. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB=
 .
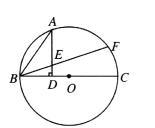
. 17. 已知Rt△ABC的两直角边的长分别为6cm和8cm,则它的外接圆的半径与内切圆半径的比为 .18. 在半径为3的圆中,长度等于3的弦所对的圆周角的度数为 .19. 如图,量角器的0度刻度线为 ,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点 ,直尺另一边交量角器于点 , ,量得 ,点 在量角器上的读数为 ,则该直尺的宽度为 .
17. 已知Rt△ABC的两直角边的长分别为6cm和8cm,则它的外接圆的半径与内切圆半径的比为 .18. 在半径为3的圆中,长度等于3的弦所对的圆周角的度数为 .19. 如图,量角器的0度刻度线为 ,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点 ,直尺另一边交量角器于点 , ,量得 ,点 在量角器上的读数为 ,则该直尺的宽度为 .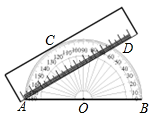
三、解答题
-
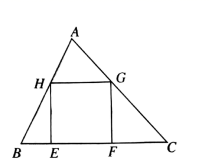
20. 计算(1)、(2)、已知 是锐角,且 ,计算 的值.21. 如下图,在 中,正方形 的两个顶点 在 上,另两个顶点 分别在 上 边上的高是 ,求正方形 的面积.
 22. 已知:如图,在菱形ABCD中,DE⊥AB于E,BE=16cm,
22. 已知:如图,在菱形ABCD中,DE⊥AB于E,BE=16cm,求此菱形的周长.