湖北省孝感市安陆市2019-2020学年七年级上学期数学期中考试试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、选择题

1. 如果80 m表示向东走80 m，则－60 m表示（）.

A、向东走60 m B、向西走60 m C、向南走60 m D、向北走60 m

查看试题解析
2. 中国的陆地面积为 $9600000 {km}^{2}$ ，把9600000用科学记数法表示为（）

A、 $96 \times 10^{5}$ B、 $0.96 \times 10^{7}$ C、 $9.6 \times 10^{5}$ D、 $9.6 \times 10^{6}$

查看试题解析
3. 若 $a$ 为任意有理数，则 $- | - a |$ 一定是（）

A、负数或零 B、负数 C、正数或零 D、正数

查看试题解析
4. $\frac{\frac{m 个 2}{2 \times 2 \times \dots \times 2}}{\frac{3 + 3 + \dots + 3}{n 个 3}}$ ＝（）

A、 $\frac{2 m}{3^{n}}$ B、 $\frac{2^{m}}{3 n}$ C、 $\frac{2^{m}}{3^{n}}$ D、 $\frac{2 m}{n^{3}}$

查看试题解析
5. 实数a，b，c，d在数轴上对应点的位置如图所示，正确的结论是( ）

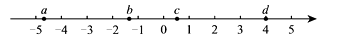A、a ＞ c B、b +c ＞ 0 C、|a|＜|d| D、-b＜d

查看试题解析
6. 计算 ${(- 4)}^{2019} \times {(- \frac{1}{4})}^{2020}$ 的结果是（）

A、4 B、－4 C、 $\frac{1}{4}$ D、 $- \frac{1}{4}$

查看试题解析
7. 某种商品进价为m元，商店将价格提高30%作零售价销售．在销售旺季过后，商店又以8折（即售价的80%）的价格开展促销活动．这时一件该商品的售价为（）

A、m元 B、0.8m元 C、1.04m元 D、0.92m元

查看试题解析
8. 已知 $y = a x^{5} + b x^{3} + c x - 5$ ，当 $x = 3$ 时， $y = 7$ ，那么 $x = - 3$ 时， $y =$ （）

A、－3 B、－7 C、－17 D、7

查看试题解析
9. 当式子|x+1|+|x﹣6|取得最小值时，x的取值范围为（）

A、﹣1≤x＜6 B、﹣1≤x≤6 C、x=﹣1或x=6 D、﹣1＜x≤6

查看试题解析
10. 观察下列各式： $3^{1} = 3$ ， $3^{2} = 9$ ， $3^{3} = 27$ ， $3^{4} = 81$ ， $3^{5} = 243$ ， $3^{6} = 729$ ， $3^{7} = 2187$ ， $3^{8} = 6561$ ……根据上述算式中的规律，猜想 $3^{2019}$ 的末位数字是（）

A、3 B、9 C、7 D、1

查看试题解析

二、填空题

11. 已知 $- a = 8$ ，则 $a =$ .

查看试题解析
12. 某公交车原坐18人，经过3个站点时上下车情况如下（上车为正，下车为负）： $(+ 3, - 8)$ ， $(+ 5, - 7)$ ， $(+ 4, - 2)$ ，则现在车上还有.

查看试题解析
13. 在数﹣5，4，﹣3，6，﹣2中任取三个数相乘，其中最大的积是.

查看试题解析
14. 计算： $(- 12) \div (\frac{1}{2} + \frac{1}{3} - \frac{1}{4} - \frac{1}{6}) =$ .

查看试题解析
15. 已知： $m^{2} + 2 m n = 13$ ， $3 m n + 2 n^{2} = 21$ ，则 $2 m^{2} + 13 m n + 6 n^{2} - 44$ 值为.

查看试题解析
16. 如图，下列各图形中的三个数之间均具有相同的规律．根据此规律，当m=99时，则M的值为．

查看试题解析

三、解答题

17. 计算：

(1)、 $(- 3) - (+ 8) - (- 6) + (+ 7)$

(2)、 $- 1^{4} - \frac{1}{6} \times [2 - {(- 3)}^{2}] \div (- 7)$

查看试题解析
18. 化简求值

(1)、 $5 x^{2} - 4 - 3 x^{2} - 5 x - 2 x^{2} - 5 + 6 x$ ，其中 $x = - 3$

(2)、 $3 x^{2} y + 2 x y - [3 x^{2} y - 2 (x y^{2} + 2 x y)] - 4 x y^{2}$ ，其中 $x$ ， $y$ 满足 ${(x + 2)}^{4} + | y - 3 | = 0$

查看试题解析

19. 某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):

星期	一	二	三	四	五	六	日
增减/辆	-1	+3	-2	+4	+7	-5	-10

(1)、生产量最多的一天比生产量最少的一天多生产多少辆?

(2)、本周总的生产量是多少辆?

查看试题解析

20. 阅读下面的计算过程，体会“拆项法”.
计算： $- 5 \frac{5}{6} + (- 9 \frac{2}{3}) + 17 \frac{3}{4} + (- 3 \frac{1}{2})$ .

解：原式 $= [(- 5) + (- 9) + 17 + (- 3)] + [(- \frac{5}{6}) + (- \frac{2}{3}) + \frac{3}{4} + (- \frac{1}{2})]$

$= 0 + (- 1 \frac{1}{4}) = - 1 \frac{1}{4}$

启发应用：

用上面的方法完成下列计算： $(- 3 \frac{3}{10}) + (- 1 \frac{1}{2}) + 2 \frac{3}{5} - (- 2 \frac{1}{2})$

查看试题解析
21. 某商场将进货价为30元的台灯以40元的销售价售出，平均每月能售出600个.市场调研表明：当销售价每上涨1元时，其销售量将减少10个.

(1)、设每个台灯的销售价上涨a元，试用含a的式子填空：
①涨价后，每个台灯的销售价为元；

②涨价后，每个台灯的利润为元；

③涨价后，台灯平均每月的销售量为台.

(2)、商场要想让销售利润平均每月达到10 000元，经理甲说：“在原售价每台40元的基础上再上涨
40元，可以完成任务.”经理乙说：“不用涨那么多，在原售价每台40元的基础上再上涨10元就可以了.”判断经理甲与经理乙的说法是否正确，并说明理由.

查看试题解析
22. 观察下列各式：
$- 1 \times \frac{1}{2} = - 1 + \frac{1}{2}$

$- \frac{1}{2} \times \frac{1}{3} = - \frac{1}{2} + \frac{1}{3}$

$- \frac{1}{3} \times \frac{1}{4} = - \frac{1}{3} + \frac{1}{4}$

…

(1)、你能探索出什么规律？（用文字或表达式）；

(2)、试运用你发现的规律计算：
$(- 1 \times \frac{1}{2}) + (- \frac{1}{2} \times \frac{1}{3}) + (- \frac{1}{3} \times \frac{1}{4}) + \cdot \cdot \cdot + (- \frac{1}{2018} \times \frac{1}{2019}) + (- \frac{1}{2019} \times \frac{1}{2020})$

查看试题解析
23. 世界杯比赛中，根据场上攻守形势，守门员会在门前来回跑动，如果以球门线为基准，向前跑记作正数，返回则记作负数，一段时间内，某守门员的跑动情况记录如下（单位：m）：+10，﹣2，+5，﹣6，+12，﹣9，+4，﹣14.（假定开始计时时，守门员正好在球门线上）

(1)、守门员最后是否回到球门线上？

(2)、守门员离开球门线的最远距离达多少米？

(3)、如果守门员离开球门线的距离超过10米（不包括10米），则对方球员挑射极可能造成破门.请问在这一时间段内，对方球员有几次挑射破门的机会？

查看试题解析
24. 已知 $| x | = 5$ ， $| y | = 3$

(1)、若 $x - y = | x - y |$ ，求 $x + y$ 的值；

(2)、若 $| x y | = - x y$ ，求 $| x - y |$ 的值；

(3)、求 $2 x - 3 y$ 的值.

查看试题解析