江苏省苏州市五校2019-2020学年高三上学期数学12月月考试卷

试卷更新日期：2020-09-27 类型：月考试卷

进入出卷网下载

一、填空题

1. 已知 $A = {- 1, 0, 1, 2}$ ， $B = {x \in R | 0 \leq x < 2}$ ，则 $A \cap B =$ .

查看试题解析
2. 若复数 $(3 - 4 i) z = 1$ （ $i$ 为虚数），则复数 $z$ 的模 $| z | =$ .

查看试题解析
3. 某市有中外合资企业160家，私营企业320家，国有企业240家，其他性质的企业80家，为了了解企业的管理情况，现用分层抽样的方法从这800家企业中抽取一个容量为 $n$ 的样本，已知从国有企业中抽取了12家，那么 $n =$ .

查看试题解析
4. 函数 $y = \sqrt{2 - x}$ 的定义域是.

查看试题解析
5.
如图所示的流程图的运行结果是

查看试题解析
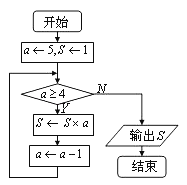6. 高三（5）班演讲兴趣小组有女生3人，男生2人，现从中任选2 名学生去参加校演讲比赛，则参赛学生恰好为1名男生和1名女生的概率是.

查看试题解析
7. 在平面直角坐标系 $x O y$ 中，直线 $x + 2 y = 0$ 为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的一条渐近线，则该双曲线的离心率为.

查看试题解析
8. 已知 $\cos (θ + \frac{π}{4}) = \frac{\sqrt{5}}{5}$ ， $θ \in (0, \frac{π}{2})$ ，则 $\sin (2 θ - \frac{π}{4})$ 的值为.

查看试题解析
9. 设公比不为1的等比数列 ${a_{n}}$ 满足 $a_{1} a_{2} a_{3} = - 1$ ，且 $a_{2}$ ， $a_{4}$ ， $a_{3}$ 成等差数列，则数列 ${a_{n}}$ 的前4项和为.

查看试题解析
10. 曲线 $f (x) = \sqrt{x} + 1$ 在点 $(4 ， 3)$ 处的切线与直线 $a x - y + 1 = 0$ 互相垂直，则实数 $a$ 的值为.

查看试题解析
11. 已知 $a > 2 b > 0$ ，且 $a + b = 1$ ，则 $\frac{2}{a - 2 b} + \frac{4}{b}$ 的最小值为.

查看试题解析
12. 已知直线 $a x + y - 2 = 0$ 与圆心为 $C$ 的圆 ${(x - 1)}^{2} + {(y - a)}^{2} = 4$ 相交于 $A, B$ 两点，且 $Δ A B C$ 为等边三角形，则实数 $a =$ ．

查看试题解析
13. 已知平面向量 $\overset{⇀}{a}$ ， $\overset{⇀}{b}$ ， $\overset{⇀}{c}$ 满足 $| \overset{⇀}{a} | = \sqrt{3}$ ， $| \overset{⇀}{b} | = 2$ ， $\overset{⇀}{a}$ ， $\overset{⇀}{b}$ 的夹角等于 $\frac{π}{6}$ ，且 $(\overset{⇀}{a} - \overset{⇀}{c}) \cdot (\overset{⇀}{b} - \overset{⇀}{c}) = 0$ ，则 $| \overset{⇀}{c} |$ 的取值范围是.

查看试题解析
14. 关于 $x$ 的方程 $| \ln x | + a = \frac{1}{2} x$ 有3个不同的实数解，则实数 $a$ 的取值范围为.

查看试题解析

二、解答题

15. 在三角形ABC中，角A,B,C的对边分别为a,b,c，若 $\sin A = \frac{3}{5}, \tan (A - B) = \frac{1}{3}$ ，角 $C$ 为钝角， $b = 5.$

(1)、求 $\sin B$ 的值；

(2)、求边 $c$ 的长.

查看试题解析
16. 如图所示，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A A_{1} B_{1} B$ 为正方形， $B B_{1} C_{1} C$ 是菱形，平面 $A A_{1} B_{1} B ⊥$ 平面 $B B_{1} C_{1} C$ ．

(1)、求证： $B C / /$ 平面 $A B_{1} C_{1}$ ；

(2)、求证： $B_{1} C ⊥ A C_{1}$ .

查看试题解析
17. 已知椭圆 $E$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，且过点 $P (\frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2})$ ．右焦点为 $F$ ．

(1)、求椭圆 $E$ 的方程；

(2)、设过右焦点为 $F$ 的直线与椭圆交于 $A$ ， $B$ 两点，且 $\overset{⇀}{A F} = 3 \overset{⇀}{F B}$ ，求直线 $A B$ 的方程．

查看试题解析
18. 如图，两座建筑物 $A B$ ， $C D$ 的底部都在同一个水平面上，且均与水平面垂直，它们的高度分别是 $10 m$ 和 $20 m$ ，从建筑物 $A B$ 的顶部 $A$ 看建筑物 $C D$ 的视角 $∠ C A D = 60 °$ ．

(1)、求 $B C$ 的长度；

(2)、在线段 $B C$ 上取一点 $P$ （点 $P$ 与点 $B$ ， $C$ 不重合），从点 $P$ 看这两座建筑物的视角分别为 $∠ A P B = α$ ， $∠ D P C = β$ ，问点 $P$ 在何处时， $α + β$ 最小？

查看试题解析
19. 已知数列 ${a_{n}}$ 、 ${b_{n}}$ 满足： $a_{1} = \frac{1}{4}$ ， $a_{n} + b_{n} = 1$ ， $b_{n + 1} = \frac{b_{n}}{1 - a_{n}^{2}}$ .

(1)、证明： ${\frac{1}{b_{n} - 1}}$ 是等差数列，并求数列 ${b_{n}}$ 的通项公式；

(2)、设 $S_{n} = a_{1} a_{2} + a_{2} a_{3} + a_{3} a_{4} + \cdot \cdot \cdot + a_{n} a_{n + 1}$ ，求实数 $a$ 为何值时 $4 a S_{n} < b_{n}$ 恒成立．

查看试题解析
20. 已知函数 $f (x) = \frac{x}{\ln x}$ ．

(1)、若曲线 $y = f (x)$ 在点 $(x_{0} ， f (x_{0}))$ 处的切线方程为 $2 x + y = a$ ，求 $x_{0}$ 的值；

(2)、当 $x > 1$ 时，求证： $f (x) > \ln x$ ；

(3)、设函数 $F (x) = f (x) - b \ln x$ ，其中 $b$ 为实常数，试讨论函数 $F (x)$ 的零点个数，并证明你的结论．

查看试题解析
21. 已知矩阵 $A = [\begin{matrix} a & b \\ 1 & 4 \end{matrix}]$ ，若矩阵 $A$ 属于特征值1的一个特征向量为 $α_{1} = [\begin{matrix} 3 \\ - 1 \end{matrix}]$ ，属于特征值5的一个特征向量为 $α_{2} = [\begin{matrix} 1 \\ 1 \end{matrix}]$ ．求矩阵 $A$ ，并写出 $A$ 的逆矩阵．

查看试题解析
22. 在极坐标系(ρ,θ)(0≤θ<2π)中,求曲线ρ=2sinθ与ρcosθ=1的交点Q的极坐标.

查看试题解析
23. 在三棱锥 $S - A B C$ 中，底面是边长为 $2 \sqrt{3}$ 的正三角形，点 $S$ 在底面 $A B C$ 上的射影 $O$ 恰是 $B C$ 的中点，侧棱 $S A$ 和底面成 $45 °$ 角．

(1)、若 $D$ 为侧棱 $S A$ 上一点，当 $\frac{S D}{D A}$ 为何值时， $B D ⊥ A C$ ；

(2)、求二面角 $S - A C - B$ 的余弦值大小．

查看试题解析
24. 已知 ${(x + 1)}^{n} = a_{0} + a_{1} (x - 1) + a_{2} {(x - 1)}^{2} + a_{3} {(x - 1)}^{3} + \cdot \cdot \cdot + a_{n} {(x - 1)}^{n}$ （其中 $n \in N^{*}$ ）.

(1)、当 $n = 6$ 时，计算 $a_{0}$ 及 $a_{1} + a_{3} + a_{5}$ ；

(2)、记 $S_{n} = a_{1} + a_{2} + \dots + a_{n}$ ，试比较 $S_{n}$ 与 $(n - 2) 2^{n} + 2 n^{2}$ 的大小，并说明理由．

查看试题解析