山东省济宁市汶上县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 方程 的解为( )A、 B、 C、 D、2. 下列手机手势解锁图案中,是中心对称图形的是( )A、
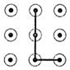 B、
B、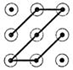 C、
C、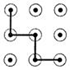 D、
D、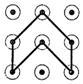 3. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根为0,则a值为( )A、1 B、﹣1 C、±1 D、04. 将抛物线 向上平移 个单位后得到的抛物线恰好与 轴有一个交点,则a的值为( )A、-1 B、1 C、-2 D、25. 如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于( )
3. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根为0,则a值为( )A、1 B、﹣1 C、±1 D、04. 将抛物线 向上平移 个单位后得到的抛物线恰好与 轴有一个交点,则a的值为( )A、-1 B、1 C、-2 D、25. 如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于( ) A、30° B、35° C、40° D、50°6. 风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是( )
A、30° B、35° C、40° D、50°6. 风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是( )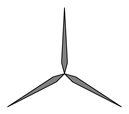
 A、45 B、60 C、90 D、1207. 一次酒会上,每两人都只碰一次杯,一共碰杯 55 次,设参加酒会的人数为x,则可列方程为( )A、 x(x﹣1)=55 B、x(x﹣1)=55 C、 x(x+1)=55 D、x(x+1)=558. 设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线 上的三点,则y1 , y2 , y3的大小关系为( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y3>y1>y29. 二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0. 其中正确的是( )
A、45 B、60 C、90 D、1207. 一次酒会上,每两人都只碰一次杯,一共碰杯 55 次,设参加酒会的人数为x,则可列方程为( )A、 x(x﹣1)=55 B、x(x﹣1)=55 C、 x(x+1)=55 D、x(x+1)=558. 设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线 上的三点,则y1 , y2 , y3的大小关系为( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y3>y1>y29. 二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0. 其中正确的是( ) A、①④ B、②④ C、①②③ D、①②③④10. 如图,在 中,顶点 , , ,将 与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转 ,则第70次旋转结束时,点D的坐标为( )
A、①④ B、②④ C、①②③ D、①②③④10. 如图,在 中,顶点 , , ,将 与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转 ,则第70次旋转结束时,点D的坐标为( ) A、 B、 C、 ) D、
A、 B、 C、 ) D、二、填空题
-
11. 点( ,2)关于原点对称的点的坐标是.12. 已知关于x的方程x2+px+q=0的两根为﹣3和﹣1,则p= , q= .13. 如图是抛物线 y=ax +bx+c 的一部分,其对称轴为直线 x=2,若其与 x 轴的一个交点为(5,0),则由图象可知,不等式 ax +bx+c<0 的解集是 .
 14. 如图,△ABC内接于☉O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若☉O的半径为2,则CD的长为
14. 如图,△ABC内接于☉O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若☉O的半径为2,则CD的长为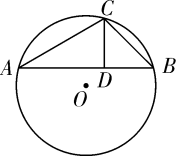 15. 如图,将 的斜边AB绕点A顺时针旋转 得到AE,直角边AC绕点A逆时针旋转 得到AF,连结EF.若 , ,且 ,则 .
15. 如图,将 的斜边AB绕点A顺时针旋转 得到AE,直角边AC绕点A逆时针旋转 得到AF,连结EF.若 , ,且 ,则 .
三、解答题
-
16. 如图,在 ,且点B的坐标为 ,点A的坐标为 .
 (1)、画出 关于点O成中心对称的 ,并写出点 的坐标;(2)、求出以点 为顶点,并经过点A的二次函数关系式.17. 已知 , 分别与 相切于点 , , , 为 上一点.
(1)、画出 关于点O成中心对称的 ,并写出点 的坐标;(2)、求出以点 为顶点,并经过点A的二次函数关系式.17. 已知 , 分别与 相切于点 , , , 为 上一点.
(Ⅰ)如图①,求 的大小;
(Ⅱ)如图②, 为 的直径, 与 相交于点 ,若 ,求 的大小.
18. 关于x的一元二次方程 有两个不相等的实数根 , .(1)、求实数m的取值范围;(2)、是否存在实数m,使得 成立?如果存在,求出m的值,如果不存在,请说明理由.19. 如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为x m,窗户的透光面积为y m2(铝合金条的宽度不计). (1)、求出y与x的函数关系式;(2)、如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.20. 在平面内,给定不在同一条直线上的点 (如图所示),点 到点 的距离均等于 ( 为常数),到点 的距离等于 的所有点组成图形 , 的平分线交图形 于点 ,连接 .
(1)、求出y与x的函数关系式;(2)、如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.20. 在平面内,给定不在同一条直线上的点 (如图所示),点 到点 的距离均等于 ( 为常数),到点 的距离等于 的所有点组成图形 , 的平分线交图形 于点 ,连接 . (1)、求证:AD=CD;(2)、过点 作 ,垂足为 ,作 ,垂足为 ,延长 交图形 于点 ,连接 .若 ,求直线 与图形 的公共点个数.21. 如图, 的两直角边 , 分别在 轴的负半轴和 轴的正半轴上, 为坐标原点, , 两点的坐标分别为 、 ,抛物线 经过点 ,且顶点在直线 上.
(1)、求证:AD=CD;(2)、过点 作 ,垂足为 ,作 ,垂足为 ,延长 交图形 于点 ,连接 .若 ,求直线 与图形 的公共点个数.21. 如图, 的两直角边 , 分别在 轴的负半轴和 轴的正半轴上, 为坐标原点, , 两点的坐标分别为 、 ,抛物线 经过点 ,且顶点在直线 上. (1)、求抛物线对应的函数关系式;(2)、若 是由 沿 轴向右平移得到的,当四边形 是菱形时,试判断点 和点 是否在该抛物线上,并说明理由;(3)、在(2)的条件下,若 点是 所在直线下方抛物线上的一个动点,过点 作 平行于 轴交 于 .设点 的横坐标为 , 的长度为 .求 与 之间的函数关系式,写出自变量 的取值范围,并求 取最大值时,点 的坐标.
(1)、求抛物线对应的函数关系式;(2)、若 是由 沿 轴向右平移得到的,当四边形 是菱形时,试判断点 和点 是否在该抛物线上,并说明理由;(3)、在(2)的条件下,若 点是 所在直线下方抛物线上的一个动点,过点 作 平行于 轴交 于 .设点 的横坐标为 , 的长度为 .求 与 之间的函数关系式,写出自变量 的取值范围,并求 取最大值时,点 的坐标.