山东省济南市章丘区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 如图所示是某几何体从三个方向看到的图形,则这个几何体是( )
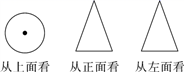 A、三棱锥 B、圆柱 C、球 D、圆锥2. 下列方程一定是一元二次方程的是( )A、 B、 C、 D、3. 两个人的影子在两个相反的方向,这说明( )A、他们站在阳光下 B、他们站在路灯下 C、他们站在路灯的两侧 D、他们站在月光下4. 若 ,则 的值为( )A、5 B、 C、-5 D、5. 若 是方程 的一个根,则 的值是( )A、1 B、 C、 D、6. 如图,下列四个三角形中,与 相似的是( )
A、三棱锥 B、圆柱 C、球 D、圆锥2. 下列方程一定是一元二次方程的是( )A、 B、 C、 D、3. 两个人的影子在两个相反的方向,这说明( )A、他们站在阳光下 B、他们站在路灯下 C、他们站在路灯的两侧 D、他们站在月光下4. 若 ,则 的值为( )A、5 B、 C、-5 D、5. 若 是方程 的一个根,则 的值是( )A、1 B、 C、 D、6. 如图,下列四个三角形中,与 相似的是( )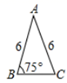 A、
A、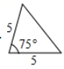 B、
B、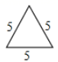 C、
C、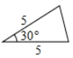 D、
D、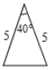 7. 用配方法解下列方程时,配方有错误的是( )A、 化为 B、 化为 C、 化为 D、 化为8. 在同一平面直角坐标系内,如果直线 与双曲线 没有交点,那么 和 的关系一定是( ).A、 , B、 , C、 , 同号 D、 , 异号9. 如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2 , 则道路的宽应为多少米?设道路的宽为x米,则可列方程为( )
7. 用配方法解下列方程时,配方有错误的是( )A、 化为 B、 化为 C、 化为 D、 化为8. 在同一平面直角坐标系内,如果直线 与双曲线 没有交点,那么 和 的关系一定是( ).A、 , B、 , C、 , 同号 D、 , 异号9. 如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2 , 则道路的宽应为多少米?设道路的宽为x米,则可列方程为( )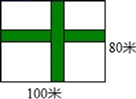 A、100×80﹣100x﹣80x=7644 B、(80﹣x)+x2=7644 C、(80﹣x)(100-x)=7644 D、100x+80x=35610. 如图,Rt△ABC中, , , ,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿AB向B点运动,设E点的运动时间为t秒,连接DE,当以B、D、E为顶点的三角形与△ABC相似时,t的值为( )
A、100×80﹣100x﹣80x=7644 B、(80﹣x)+x2=7644 C、(80﹣x)(100-x)=7644 D、100x+80x=35610. 如图,Rt△ABC中, , , ,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿AB向B点运动,设E点的运动时间为t秒,连接DE,当以B、D、E为顶点的三角形与△ABC相似时,t的值为( )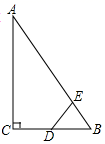 A、2或3.5 B、2或3.2 C、2或3.4 D、3.2或3.411. 如图,在△ABC中,中线BE、CD相交于点O , 连接DE , 下列结论:① ;② ;③ ;④ ;其中正确的个数有( )
A、2或3.5 B、2或3.2 C、2或3.4 D、3.2或3.411. 如图,在△ABC中,中线BE、CD相交于点O , 连接DE , 下列结论:① ;② ;③ ;④ ;其中正确的个数有( )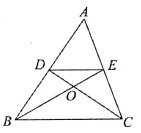 A、1个 B、2个 C、3个 D、4个12. 如图,在 轴正半轴上依次截取 ,过点 、 、 、…… 分别作 轴的垂线,与反比例函数 交于点 、 、 、…、 ,连接 、 、… ,过点 、 、…、 分别向 、 、…、 作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于( ).
A、1个 B、2个 C、3个 D、4个12. 如图,在 轴正半轴上依次截取 ,过点 、 、 、…… 分别作 轴的垂线,与反比例函数 交于点 、 、 、…、 ,连接 、 、… ,过点 、 、…、 分别向 、 、…、 作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于( ).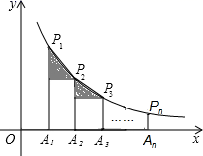 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
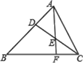
13. 方程x(x+2)=2(x+2) 的解是 .14. 在一个不透明的盒子里装有除颜色外其余均相同的2个黄色兵乓球和若干个白色兵乓球,从盒子里随机摸出一个兵乓球,摸到黄色兵乓球的概率为 ,那么盒子内白色兵乓球的个数为.15. 如图,在 中, , 为 的中点, 的延长线交 于点 ,则 .
 16. 一个几何体的三视图如图所示,这个几何体的侧面积为 .
16. 一个几何体的三视图如图所示,这个几何体的侧面积为 .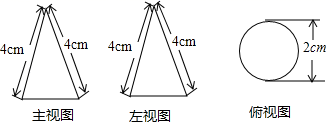 17. 如图,在 中, , 两个顶点在 轴的上方,顶点 的坐标是 .以点 为位似中心,在 轴的下方作 的位似图形 ,并且 是把 放大到原来的2倍后得到的设点 的对应点 的横坐标是 ,则点 的横坐标是 .
17. 如图,在 中, , 两个顶点在 轴的上方,顶点 的坐标是 .以点 为位似中心,在 轴的下方作 的位似图形 ,并且 是把 放大到原来的2倍后得到的设点 的对应点 的横坐标是 ,则点 的横坐标是 .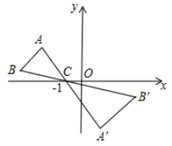 18. 如图,已知点A是一次函数 (x≥0)图象上一点,过点A作x轴的垂线l , B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC , 反比例函数 (x>0)的图象过点B , C , 若△OAB的面积为6,则△ABC的面积是 .
18. 如图,已知点A是一次函数 (x≥0)图象上一点,过点A作x轴的垂线l , B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC , 反比例函数 (x>0)的图象过点B , C , 若△OAB的面积为6,则△ABC的面积是 .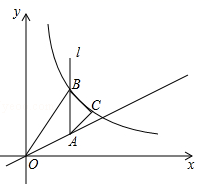
三、解答题
-
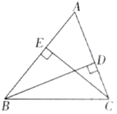
19. 解方程:(1)、 ;(2)、 (用配方法解)20. 如图, , 是 的高.求证: .
 21. 已知关于x的一元二次方程mx2−(m+1)x+1=0.(1)、求证:此方程总有两个实数根;(2)、若m为整数,当此方程的两个实数根都是整数时,求m的值.22. 如图,在 中, , , ,点P由点A出发沿 方向向终点B以每秒 的速度匀速移动,点Q由点B出发沿 方向向终点C以每秒 的速度匀速移动,速度为 .如果动点同时从点A,B出发,当点P或点Q到达终点时运动停止.则当运动几秒时,以点Q,B,P为顶点的三角形与 相似?
21. 已知关于x的一元二次方程mx2−(m+1)x+1=0.(1)、求证:此方程总有两个实数根;(2)、若m为整数,当此方程的两个实数根都是整数时,求m的值.22. 如图,在 中, , , ,点P由点A出发沿 方向向终点B以每秒 的速度匀速移动,点Q由点B出发沿 方向向终点C以每秒 的速度匀速移动,速度为 .如果动点同时从点A,B出发,当点P或点Q到达终点时运动停止.则当运动几秒时,以点Q,B,P为顶点的三角形与 相似?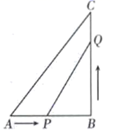 23. 某商场销售某种冰箱,每台进货价为2500元,标价为3000,(1)、若商场连续两次降价,每次降价的百分率相同,最后以2430元售出,求每次降价的百分率;(2)、市场调研表明:当每台售价为2900元时,平均每天能售出8台,当每台售价每降50元时,平均每天就能多售出4台,若商场要想使这种冰箱的销售利润平均每天达到5000元,则每台冰箱的定价应为多少元?24. 如图所示,网格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的 是格点三角形.在建立平面直角坐标系后,点 的坐标为 .
23. 某商场销售某种冰箱,每台进货价为2500元,标价为3000,(1)、若商场连续两次降价,每次降价的百分率相同,最后以2430元售出,求每次降价的百分率;(2)、市场调研表明:当每台售价为2900元时,平均每天能售出8台,当每台售价每降50元时,平均每天就能多售出4台,若商场要想使这种冰箱的销售利润平均每天达到5000元,则每台冰箱的定价应为多少元?24. 如图所示,网格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的 是格点三角形.在建立平面直角坐标系后,点 的坐标为 .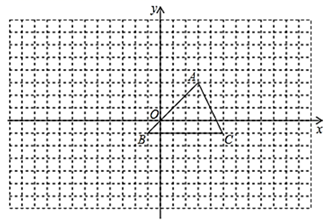 (1)、把 向下平移5格后得到 ,写出点 , , 的坐标,并画出 ;(2)、把 绕点 按顺时针方向旋转 后得到 ,写出点 , , 的坐标,并画出 ;(3)、把 以点 为位似中心放大得到 ,使放大前后对应线段的比为 ,写出点 , , 的坐标,并画出 .25. 某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况,进行了统计调查 随机调查了某班所有同学最喜欢的节目 每名学生必选且只能选择四类节目中的一类 并将调查结果绘成如下不完整的统计图 根据两图提供的信息,回答下列问题:
(1)、把 向下平移5格后得到 ,写出点 , , 的坐标,并画出 ;(2)、把 绕点 按顺时针方向旋转 后得到 ,写出点 , , 的坐标,并画出 ;(3)、把 以点 为位似中心放大得到 ,使放大前后对应线段的比为 ,写出点 , , 的坐标,并画出 .25. 某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况,进行了统计调查 随机调查了某班所有同学最喜欢的节目 每名学生必选且只能选择四类节目中的一类 并将调查结果绘成如下不完整的统计图 根据两图提供的信息,回答下列问题: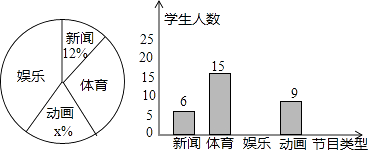 (1)、最喜欢娱乐类节目的有人,图中 ;
(1)、最喜欢娱乐类节目的有人,图中 ;
(2)、请补全条形统计图;
(3)、根据抽样调查结果,若该校有1800名学生,请你估计该校有多少名学生最喜欢娱乐类节目;(4)、在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.26. 根据下图回答问题: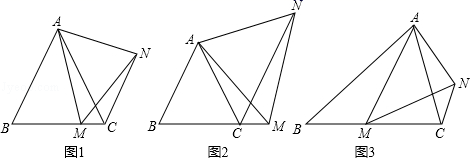 (1)、(提出问题)
(1)、(提出问题)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
(2)、(类比探究)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
(3)、(拓展延伸)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
27. 如图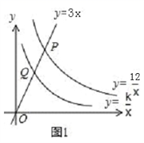
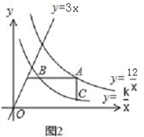
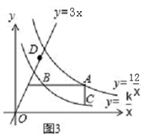
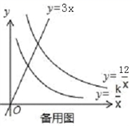
如图1,已知直线y=3x分别与双曲线y= 、y= (x>0)交于P、Q两点,且OP=2OQ .
(1)、求k的值.(2)、如图2,若点A是双曲线y= 上的动点,AB∥x轴,AC∥y轴,分别交双曲线y= (x>0)于点B、C , 连接BC.请你探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;(3)、如图3,若点D是直线y=3x上的一点,请你进一步探索在点A运动过程中,以点A、B、C、D为顶点的四边形能否为平行四边形?若能,求出此时点A的坐标;若不能,请说明理由.