湖北省黄石市下陆区2019-2020学年七年级上学期数学期中考试试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、选择题

1. -2的相反数是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 太阳的半径大约是669000千米，用科学记数法表示669000结果是（）

A、6.69×10³ B、6.69×10⁴ C、6.69×10⁵ D、6.69×10⁶

查看试题解析
3. 下列各组单项式中,不是同类项的一组是（）

A、 $x^{2} y$ 和 $2 x y^{2}$ B、 $3 x y$ 和 $- \frac{x y}{2}$ C、 $5 x^{2} y$ 和 $- 2 y x^{2}$ D、 $- 3^{2}$ 和3

查看试题解析
4. 单项式﹣ $\frac{2}{3}$ a²b的系数和次数分别是（）

A、 $\frac{2}{3}$ ，2 B、 $\frac{2}{3}$ ，3 C、﹣ $\frac{2}{3}$ ，2 D、﹣ $\frac{2}{3}$ ，3

查看试题解析
5. 下列各组运算中，运算中结果相同的是（）

A、 $2^{3}$ 和 $3^{2}$ B、 ${(- 4)}^{3}$ 和 $- 4^{3}$ C、 ${(- 5)}^{2}$ 和 $- 5^{5}$ D、 ${(- \frac{2}{3})}^{2}$ 和 ${(- \frac{3}{2})}^{3}$

查看试题解析
6. 下列各式中，运算正确的是（）

A、3a＋2b＝5ab B、3a²b－3ba²＝0 C、a³＋a²＝a⁵ D、5a²－4a²＝1

查看试题解析
7. 若 $| m - 3 | + {(n + 2)}^{2} = 0$ ，则 $m + n$ 的值为（）

A、-5 B、-1 C、1 D、5

查看试题解析
8. 已知a=3.50是由四舍五入得到的近似数，则a的可能取值范围是（）

A、3.45≤a<3.55 B、3.495≤a＜3.505 C、3.495≤a≤3.505 D、3.49 5＜a＜3.505

查看试题解析
9. 已知a<0、b>0且│a∣>│b∣，则a、b、-a、-b的大小关系是（）

A、b>-a>a>-b B、-b>a>-a>b C、a>-b>-a>b D、-a>b>-b >a

查看试题解析
10. 下列图案由边长相等的黑、白两色正方形按一定规律拼接而成，依此规律，第10个图形中白色正方形的个数为（）

A、20 B、30 C、32 D、34

查看试题解析

二、填空题

11. 温度由 $- 4^{°} C$ 上升 $7^{°} C$ 是 $^{°} C$

查看试题解析
12. 多项式2a²b﹣πab²﹣ab的次数为.

查看试题解析
13. 下列整式﹣ $\frac{1}{2}$ x²y， $\frac{m^{4} n^{2}}{7}$ ，x²+y²﹣1，﹣5，x，2﹣y中有a个单项式，b个多项式，则a^b＝.

查看试题解析
14. 有理数 $a$ 、 $b$ 、 $c$ 在数轴上位置如图，则 $| c - a | - | a - b | - | b + c |$ 的值为 .

查看试题解析
15. 按一定规律排列的一列数依次为 $\frac{1}{2}$ ， $- \frac{1}{5}$ ， $\frac{1}{10}$ ， $- \frac{1}{17}$ ， $\frac{1}{26}$ ， $- \frac{1}{37}$ ，……，按此规律排列下去，这列数中第8个数是.

查看试题解析
16. 某部门组织调运一批物资从 $A$ 地到 $B$ 地，一运送物资车从 $A$ 地出发，出发第一小时内按60千米/小时匀速行驶，一小时后以原来速度的1.5倍匀速行驶，并比原计划提前20分钟到达目的地.设 $A$ 地到 $B$ 地距离为 $x$ 千米，则根据题意得原计划规定的时间为(用含 $x$ 的代数式表示)：小时.

查看试题解析

三、解答题

17. 计算：

(1)、 $3 + (- 11) - (- 9)$

(2)、 $- 1^{4} + \frac{1}{4} \times [2 \times (- 6) - {(- 4)}^{2}]$

(3)、 $- 2^{3} \times [(- \frac{2}{3}) + \frac{1}{2}] - 6 \times {(- \frac{2}{3})}^{2} \div \frac{2}{3} - (\frac{3}{8} + \frac{1}{6} - \frac{3}{4}) + (- \frac{1}{24})$

查看试题解析
18. 化简与求值

(1)、 $- 3 x y - 2 y^{2} + 5 x y - 4 y^{2}$

(2)、 $2 (5 a^{2} - 2 a) - 4 (- 3 a + 2 a^{2})$

(3)、先化简，再求值： $x^{2} - 3 (2 x^{2} - 4 y) + 2 (x^{2} - y)$ 其中 $x = - 2 ， y = \frac{1}{5}$

查看试题解析
19. 已知 $a ， b$ 互为相反数， $c ， d$ 互为倒数， $m$ 的倒数等于本身.求代数式 $- 2 (a + b) - \frac{c d}{2019} + \frac{m^{2}}{2019}$ 的值.

查看试题解析
20. 现有20筐西红柿要出售，从中随机抽取6筐西红柿，以每筐50千克为标准，超过的质量记为正数，不足的质量记为负数，称得的结果记录如下：-5，+3，-4，+1，+2，-3。

(1)、这6筐西红柿总计是超过或不足多少千克？

(2)、若每千克的西红柿的售价为3元，估计这批西红柿总销售额是多少？

查看试题解析
21. 定义：若 $a + b = 2$ ，则称a与b是关于1的平衡数．

(1)、3与是关于1的平衡数， $5 - x$ 与是关于1的平衡数 $. ($ 用含x的代数式表示 $)$

(2)、若 $a = 2 x^{2} - 3 (x^{2} + x) + 4$ ， $b = 2 x - [3 x - (4 x + x^{2}) - 2]$ ，判断a与b是否是关于1 的平衡数，并说明理由．

查看试题解析
22. 观察下面三行数
$- 2 ， 4 ， - 8 ， 16 ， - 32 ， 64 \dots \dots ；$ ①

$- 1 ， 2 ， - 4 ， 8 ， - 16 ， 32 \dots \dots ；$ ②

$0 ， 6 ， - 6 ， 18 ， - 30 ， 66 \dots \dots$ ③

(1)、第①行的第 $n$ 个数可表示为；

(2)、第②③行数与第①行数分别有什么关系?

(3)、取每行的第 $n$ 个数，从上到下依次把这三个数记为 $A ， B ， C$ ，当 $n = 8$ 时，求 $A + B + C$ 的值.

查看试题解析
23. 已知：A=2x²+ax﹣5y+b，B=bx²﹣ $\frac{3}{2}$ x﹣ $\frac{5}{2}$ y﹣3.

(1)、求3A﹣（4A﹣2B）的值；

(2)、当x取任意数值，A﹣2B的值是一个定值时，求（a+ $\frac{3}{14}$ A）﹣（2b+ $\frac{3}{7}$ B）的值.

查看试题解析

24. 为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收贵的价目表如下(注：水费按月份结算，

m^{3}

表示立方米)

价目表
每月用水量	价格
不超过 $6 m^{3}$ 的部分	$2 元 / m^{3}$
超出 $6 m^{3}$ 不超出 $10 m^{3}$ 的部分	$4 元 / m^{3}$
超出 $10 m^{3}$ 的部分	$6 元 / m^{3}$

(1)、某户居民1月份和2月份的用水量分别为

5 m^{3}

和

8 m^{3}

，则应收水费分别是元和元

(2)、若该户居民

3

月份用水量

a m^{3}

(其中

6 < a < 10

)，则应收水费多少元? (用含

a

的式子表示，并化简)

(3)、若该户居民

4 、 5

两个月共用水

14 m^{3}

(

5

月份用水量超过4月份)，设4月份用水

x m^{3}

，求该户居民

4 、 5

两个月共交水费多少元? (用含

x

的式子表示，并化简)

查看试题解析

25. 已知有理数 $a ， b ， c$ 在数轴上所对应的点分别是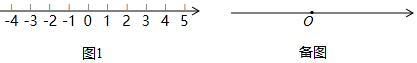 $A ， B ， C$ 三点，且 $a ， b$ 满足：①多项式 $- \frac{1}{2} x^{| a |} + (a - 2) x + 7$ 是关于 $x$ 的二次三项式：② ${(b - 1)}^{2} + | c - 5 | = 0$

(1)、请在图1的数轴上描出 $A ， B ， C$ 三点，并直接写出 $a ， b ， c$ 三数之间的大小关系(用“<”连接) ；

(2)、点 $P$ 为数轴上 $C$ 点右侧一点，且点 $P$ 到 $A$ 点的距离是到 $C$ 点距离的2倍，求点 $P$ 在数轴上所对应的有理数；

(3)、点 $A$ 在数轴上以每秒1个单位长度的速度向左运动，同时点 $B$ 和点 $C$ 在数轴上分别以每秒 $m$ 个单位长度和4个单位长度的速度向右运动(其中 $m < 4$ )，若在整个运动的过程中，点 $B$ 到点 $A$ 的距离与点 $B$ 到点 $C$ 的距离差始终不变，求 $m$ 的值.

查看试题解析