山东省济南市市中区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 用配方法解方程x2﹣2x﹣5=0时,原方程应变形为( )A、(x+1)2=6 B、(x+2)2=9 C、(x﹣1)2=6 D、(x﹣2)2=92. 根据下面表格中的对应值:
x
3.23
3.24
3.25
3.26
ax2+bx+c
-0.06
-0.02
0.03
0.09
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A、3<x<3.23 B、3.23<x<3.24 C、3.24<x<3.25 D、3.25<x<3.263. 下列说法错误的是( )A、方程 有一根为0 B、方程 的两根互为相反数 C、方程 的两根互为相反数 D、方程 无实数根4. 如图,l1∥l2∥l3 , 直线a,b与l1 , l2 , l3分别相交于点A、B、C和点D、E、F,
若 ,DE=4,则DF的长是( )
A、 B、 C、10 D、65. 下列说法正确的个数有( )个①凡正方形都相似;②凡等腰三角形都相似;③凡等腰直角三角形都相似;④两个相似多边形的面积比为4:9,则周长的比为16:81.
A、1 B、2 C、3 D、46. 如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( ) A、AB=24m B、MN∥AB C、△CMN∽△CAB D、CM:MA=1:27. 如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
A、AB=24m B、MN∥AB C、△CMN∽△CAB D、CM:MA=1:27. 如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )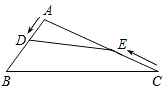 A、3秒或4.8秒 B、3秒 C、4.5秒 D、4.5秒或4.8秒8. 如果反比例函数 的图像经过点(-3,-4),那么该函数的图象位于( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限9. 如果两点P1(1,y1)和P2(2,y2)都在反比例函数y= 的图象上,那么下列正确的是( )A、y2<y1<0 B、y1<y2<0 C、y2>y1>0 D、y1>y2>010. 如图所示,直线y=x与双曲线y= (k>0)的一个交点为A,且OA=2,则k的值为( )
A、3秒或4.8秒 B、3秒 C、4.5秒 D、4.5秒或4.8秒8. 如果反比例函数 的图像经过点(-3,-4),那么该函数的图象位于( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限9. 如果两点P1(1,y1)和P2(2,y2)都在反比例函数y= 的图象上,那么下列正确的是( )A、y2<y1<0 B、y1<y2<0 C、y2>y1>0 D、y1>y2>010. 如图所示,直线y=x与双曲线y= (k>0)的一个交点为A,且OA=2,则k的值为( )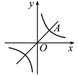 A、1 B、2 C、 D、211. 如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为( )
A、1 B、2 C、 D、211. 如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为( )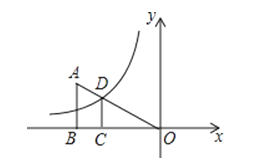 A、﹣16 B、16 C、﹣15 D、1512. 如图,在边长为2的正方形ABCD中,点E是边AD中点, 点F在边CD上,且FE⊥BE,设BD与EF交于点G,则△DEG的面积是( )
A、﹣16 B、16 C、﹣15 D、1512. 如图,在边长为2的正方形ABCD中,点E是边AD中点, 点F在边CD上,且FE⊥BE,设BD与EF交于点G,则△DEG的面积是( )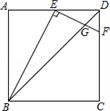 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若 ,则 =14. 如果关于x的方程x2﹣6x+m=0有两个相等的实数根,那么m= .15. 点P既在反比例函数y=- (x>0)的图象上,又在一次函数y=-x-2的图象上,则P点的坐标是.16. 反比例函数 的图象在第二、四象限,那么实数
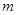 的取值范围是 . 17. 如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于 .
的取值范围是 . 17. 如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于 .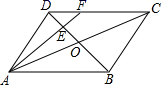 18. 如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②BG=EG;③△MFG为等腰三角形;④DE:AB=1+ :1,其中正确结论的序号为 .
18. 如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②BG=EG;③△MFG为等腰三角形;④DE:AB=1+ :1,其中正确结论的序号为 .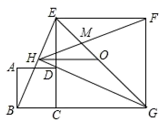
三、解答题
-
19. 解方程(1)、x2﹣4x﹣1=0;(2)、x2+3x﹣2=0;(3)、2x2+3x+3=020. 已知关于x的方程x2+(2k﹣1)x+k2﹣1=0有两个实数根x1 , x2 .(1)、求实数k的取值范围;(2)、若x1 , x2满足x12+x22=16+x1x2 , 求实数k的值.21. 某服装店出售某品牌的棉衣,进价为100元/件,当售价为150元/件时,平均每天可卖30件;为了尽快减少库存迎接“元旦”的到来,商店决定降价销售,增加利润,经调查每件降价5元,则每天可多卖10件,现要想平均每天获利2000元,且让顾客得到实惠,那么每件棉衣应降价多少元?22. 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
 (1)、求证:△ADE∽△ABC;(2)、若AD=3,AB=5,求 的值.23. 如图,点A(3,2)和点M(m,n)都在反比例函数y= (x>0)的图象上.
(1)、求证:△ADE∽△ABC;(2)、若AD=3,AB=5,求 的值.23. 如图,点A(3,2)和点M(m,n)都在反比例函数y= (x>0)的图象上. (1)、k的值为;(2)、当m=4,求直线AM的解析式;(3)、当m>3时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴与点Q,试说明四边形ABPQ是平行四边形.24. 以四边形ABCD的边AB、AD为底边分别作等腰三角形ABE 和等腰三角形ADF.
(1)、k的值为;(2)、当m=4,求直线AM的解析式;(3)、当m>3时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴与点Q,试说明四边形ABPQ是平行四边形.24. 以四边形ABCD的边AB、AD为底边分别作等腰三角形ABE 和等腰三角形ADF.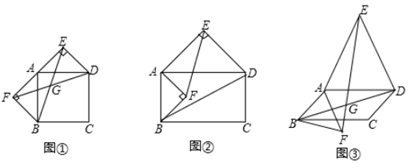 (1)、当四边形ABCD为正方形时(如图①),以边AB、AD为斜边分别向外侧作等腰直角△ABE和等腰直角△ADF , 连接BF、ED , 线段BF和ED的数量关系是;(2)、当四边形ABCD为矩形时(如图②),以边AB、AD为斜边分别向矩形内侧、外侧作等腰直角△ABE和等腰直角△ADF , 连接EF、BD , 线段EF和BD具有怎样的数量关系?请说明理由;(3)、当四边形ABCD为平行四边形时,以边AB、AD为底边分别向平行四边形内侧、外侧作等腰△ABE和等腰△ADF , 且△ABE和△ADF的顶角均为 ,连接EF、BD , 交点为G.请用 表示出∠FGD , 并说明理由.
(1)、当四边形ABCD为正方形时(如图①),以边AB、AD为斜边分别向外侧作等腰直角△ABE和等腰直角△ADF , 连接BF、ED , 线段BF和ED的数量关系是;(2)、当四边形ABCD为矩形时(如图②),以边AB、AD为斜边分别向矩形内侧、外侧作等腰直角△ABE和等腰直角△ADF , 连接EF、BD , 线段EF和BD具有怎样的数量关系?请说明理由;(3)、当四边形ABCD为平行四边形时,以边AB、AD为底边分别向平行四边形内侧、外侧作等腰△ABE和等腰△ADF , 且△ABE和△ADF的顶角均为 ,连接EF、BD , 交点为G.请用 表示出∠FGD , 并说明理由.