浙江省杭州市西湖区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 计算2^﹣²的结果是（）

A、2 B、﹣2 C、﹣4 D、 $\frac{1}{4}$

查看试题解析
2. 某种感冒病毒的直径是0.00000012米，数0.00000012用科学记数法表示为（）

A、1.2×10^﹣⁶ B、1.2×10^﹣⁷ C、1.2×10^﹣⁸ D、12×10^﹣⁸

查看试题解析
3. 将a²﹣1分解因式，结果正确的是（）

A、a （a﹣1） B、a （a+1） C、（a+1）（a﹣1） D、（a﹣1）²

查看试题解析
4. 下列调查：①日光灯管厂要检测一批灯管的使用寿命；②了解居民对废电池的处理情况；③了解初中生的主要娱乐方式；④某公司对退休职工进行健康检查，应作抽样调查的是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
5. 如图，直线l₁∥l₂ ，线段AB交l₁ ， l₂于D，B两点，过点A作AC⊥AB，交直线l₁于点C，若∠1＝15 $°$ ，则∠2＝（）

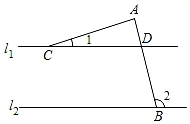A、95 $°$ B、105 $°$ C、115 $°$ D、125 $°$

查看试题解析
6. 已知分式A＝ $\frac{4}{x^{2} - 4}$ ，B＝ $\frac{1}{x + 2} + \frac{1}{2 - x}$ ，其中x≠±2，则A与B的关系是（）

A、A＝B B、A＝﹣B C、A＞B D、A＜B

查看试题解析
7. 定义新运算：a*b＝ab+a²﹣b² ，则（x+y）*（x﹣y）＝（）

A、x²﹣y² B、x²﹣y²﹣2xy C、x²﹣y²﹣4xy D、x²﹣y²+4xy

查看试题解析
8. 如图，将边长为5cm的等边三角形ABC沿边BC向右平移3cm，得到△DEF，则四边形ADFB的周长为（）cm.

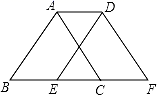A、20 B、21 C、22 D、23

查看试题解析
9. 已知2ⁿ＋2¹²＋1（n＜0）是一个有理数的平方，则n的值为（）

A、﹣16 B、﹣14 C、﹣12 D、﹣10

查看试题解析
10. 如图，直线AB∥CD，点F在直线AB上，点N在直线CD上，∠EFA＝25°，∠FGH＝90°，∠HMN＝25°，∠CNP＝30°，则∠GHM＝（）

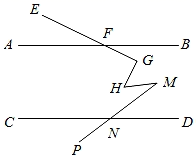A、45° B、50° C、55° D、60°

查看试题解析

二、填空题

11. 若2x﹣y＝12，用含有x的代数式表示y，则y＝.

查看试题解析
12. 如图，有下列3个结论：①能与∠DEF构成内错角的角的个数是2；②能与∠EFB构成同位角的角的个数是1；③能与∠C构成同旁内角的角的个数是4，以上结论正确的是.

查看试题解析
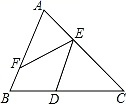13. 已知a^x＝2，a^y＝3，则a^x+y＝；a^3x^﹣^2y＝.

查看试题解析
14. 甲、乙两人练习跑步，如果乙先跑10米，则甲跑5秒就可追上乙；如果乙先跑2秒，则甲跑4秒就可追上乙，若设甲的速度为x米/秒，乙的速度为y米/秒，可列方程组.

查看试题解析
15. 已知x﹣2＝ $\sqrt{2}$ ，则代数式（x＋1）²﹣6（x＋1）＋9的值为.

查看试题解析
16. 一列数a₁ ， a₂ ， a₃ ， …，a_n ，其中a₁＝﹣1，a₂＝ $\frac{1}{1 - a_{1}}$ ，a₃＝ $\frac{1}{1 - a_{2}}$ ，…，a_n＝ $\frac{1}{1 - a_{n - 1}}$ ，则a₂＝；a₁+a₂+a₃+…+a₂₀₂₀＝；a₁×a₂×a₃×…×a₂₀₂₀＝.

查看试题解析

三、解答题

17. 计算或化简

(1)、（14a³﹣7a²）÷（7a）；

(2)、（a+b）（a²﹣ab+b²）.

查看试题解析
18. 解方程或解方程组

(1)、 ${\begin{array}{l} 3 x + 2 y = 13 \\ 3 x - 2 y = 5 \end{array}$ ；

(2)、 $\frac{x}{x - 3}$ ﹣2＝ $\frac{- 3}{3 - x}$ .

查看试题解析
19. 为了了解学生最喜欢的趣味运动项目类型：A：跳长绳，B：踢毽子，C：打篮球，D：拔河，共四类，随机抽查了部分学生，并将统计结果绘制成图①和图②的统计图（不完整）.请根据图中提供的信息，解答下列问题：

(1)、在图①中，求D部分所占扇形的圆心角的度数.

(2)、将图②补充完整.

(3)、若全校共有学生1200名，估计该校最喜欢踢毽子的学生有多少.

查看试题解析
20. 已知a²﹣3a+1＝0.

(1)、判断a＝0是否成立？请说明理由.

(2)、求6a﹣2a²的值.

(3)、求a+ $\frac{1}{a}$ 的值.

查看试题解析
21. 玲玲家准备装修一套新住房，若甲、乙两个装饰公司合作，需6周完成，共需装修费为5.2万元；若甲公司单独做4周后，剩下的由乙公司来做，还需9周才能完成，共需装修费4.8万元.玲玲的爸爸妈妈商量后决定只选一个公司单独完成.

(1)、如果从节约时间的角度考虑应选哪家公司？

(2)、如果从节约开支的角度考虑呢？请说明理由.

查看试题解析
22. 已知m＝a²b，n＝3a²﹣2ab（a≠0，a≠b）.

(1)、当a＝3，b＝﹣2时，分别求m，n的值.

(2)、比较n+ $\frac{m b}{a^{2}}$ 与2a²的大小.

(3)、当m＝12，n＝18时，求 $\frac{1}{b}$ ﹣ $\frac{2}{3 a}$ 的值.

查看试题解析
23. 将一副三角板中的两块直角三角尺的直角顶点C按照如图①的方式叠放在一起（∠A＝30°，∠ABC＝60°，∠E＝∠EDC＝45°），且三角板ACB的位置保持不动.

(1)、将三角板DCE绕点C按顺时针方向旋转至图②，若∠ACE＝60°，求∠DCB的度数.

(2)、将三角板DCE绕点C按顺时针方向旋转，当旋转到ED∥AB时，求∠BCE的度数（请先在备用图上补全相应的图形）.

(3)、当0°＜∠BCE＜180°且点E在直线BC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠BCE所有可能的值；若不存在，请说明理由.

查看试题解析