山东省德州市禹城市2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，一定是关于x的一元二次方程的是（）

A、 ${ax}^{2} + bx + c = 0$ B、 $2 (x - x^{2}) - 1 = 0$ C、 $x^{2} - y - 2 = 0$ D、 ${mx}^{2} - 3 x = x^{2} + 2$

查看试题解析
2. 剪纸艺术是中华文化的瑰宝，下列剪纸图案中，既不是中心对称图形也不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 某经济开发区今年一月份工业产值达到80亿元，第一季度总产值为275亿元，问二、三月平均每月的增长率是多少？设平均每月的增长率为x，根据题意所列方程是（　　）

A、80（1+x）²=275 B、80+80（1+x）+80（1+x）²=275 C、80（1+x）³=275 D、80（1+x）+80（1+x）²=275

查看试题解析
4. 如果一元二次方程 $x^{2} - 2 x - 3 = 0$ 的两根为 $x_{1}$ 、 $x_{2}$ ，则 $x_{1}^{2} x_{2} + x_{1} x_{2}^{2}$ 的值等于（）

A、-6 B、6 C、-5 D、5

查看试题解析
5. 二次函数 $y = - 2 x^{2} + 4 x + 1$ 的图象是如何移动就得到 $y = - 2 x^{2}$ 的图象（）

A、向左移动1个单位，向上移动3个单位 B、向右移动1个单位，向上移动3个单位 C、向左移动1个单位，向下移动3个单位 D、向右移动1个单位，向下移动3个单位

查看试题解析
6. 已知二次函数y=kx²﹣5x﹣5的图象与x轴有交点，则k的取值范围是（）

A、k>- $\frac{5}{4}$ B、k - $\frac{5}{4}$ 且k≠0 C、k $\geq$ - $\frac{5}{4}$ D、k>- $\frac{5}{4}$ 且k≠0

查看试题解析
7. 如图， $⊙ O$ 中，若 $∠ B O D = 140 °$ ， $∠ C D A = 30 °$ ，则 $∠ A E C$ 的度数是（）

A、80° B、100° C、110° D、125°

查看试题解析
8. 《九章算术》是我国古代著名数学经典，其中对勾股定理的论述比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小.以锯锯之，深一寸，锯道长一尺.问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深1寸，锯道长1尺.如图，已知弦 $A B = 1$ 尺，弓形高 $C D = 1$ 寸，（注：1尺=10寸）问这块圆柱形木材的直径是（）

A、13寸 B、6.5寸 C、20寸 D、26寸

查看试题解析
9. 若一元二次方程x²-2x-m=0无实数根，则一次函数y=（m+1）x+m-1的图象不经过第（　　）象限．

A、四 B、三 C、二 D、一

查看试题解析
10. 已知点（1，y₁）、（-2，y₂）、（-4，y₃）都是抛物线y=-2ax²-8ax+3（a＜0）图象上的点，则下列各式中正确的是（）

A、y₁＜y₃＜y₂ B、y₃＜y₂＜y₁ C、y₂＜y₃＜y₁ D、y₁＜y₂＜y₃

查看试题解析
11. 当ab＞0时，y＝ax²与y＝ax＋b的图象大致是（）

A、 B、 C、 D、

查看试题解析
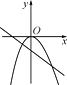12. 如图，二次函数y=ax²+bx+c（a≠0）的图象与x轴交于点A、B两点，与y轴交于点C，对称轴为直线x=-1，点B的坐标为（1，0），则下列结论：①AB=4；②b²-4ac＞0；③ab＜0；④a²-ab+ac＜0，其中正确的结论有（）个．

A、3 B、4 C、2 D、1

查看试题解析

二、填空题

13. 已知关于x的方程 $x^{2} + mx - 6 = 0$ 的一个根为2，则这个方程的另一个根是．

查看试题解析
14. 如图，AB为⊙O的直径，弦CD⊥AB，E为 $\overset{⌢}{B C}$ 上一点，若 $∠ C E A = 28 °$ ，则 $∠ A B D =$ 度.

查看试题解析

15. 二次函数

y = {ax}^{2} + bx + c (a \neq 0)

中的自变量

x

与函数值

y

的部分对应值如下表：

$x$	…	$- \frac{3}{2}$	-1	$- \frac{1}{2}$	0	$\frac{1}{2}$	1	$\frac{3}{2}$	…
$y$	…	$- \frac{5}{4}$	-2	$- \frac{9}{4}$	-2	$- \frac{5}{4}$	0	$\frac{7}{4}$	…

则 ${ax}^{2} + bx + c = 0$ 的解为．

查看试题解析

16. 如图，两块相同的三角板完全重合在一起， $∠ A = 30 °$ ， $A C = 10$ ，把上面一块绕直角顶点 $B$ 逆时针旋转到 $Δ A' B C'$ 的位置，点 $C'$ 在 $A C$ 上， $A' C'$ 与 $A B$ 相交于点 $D$ ，则 $C' D =$ .

查看试题解析
17. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ，若 $∠ B O D = 138 °$ ，则它的一个外角 $∠ D C E$ 等于.

查看试题解析
18. 二次函数y＝2x²＋mx＋8的图象如图所示，则m＝．

查看试题解析

三、解答题

19. 解方程：

(1)、x²-3x+1=0；

(2)、x（x+3）-（2x+6）=0．

查看试题解析
20. 在9×9的正方形网格中，小正方形的边长均为1．

(1)、画出将△ABC向下平移4格后的△A₁B₁C₁；

(2)、再画出△ABC绕点O逆时针旋转90º的△A₂B₂C₂；

(3)、再画出△ABC关于点O的中心对称图形△A₃B₃C₃；

(4)、求出△ABC的面积.

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $x^{2} + (2 m + 1) x + m^{2} = 0$

(1)、若方程有两个实数根，求 $m$ 的最小整数值。

(2)、若方程的两个实数根为 $x_{1}$ ， $x_{2}$ 且 ${(x_{1} - x_{2})}^{2} + m^{2} = 21$ ，求 $m$ 的值。

查看试题解析
22. 某宾馆有客房200间供游客居住，当每间客房的定价为每天180元时，客房恰好全部住满；如果每间客房每天的定价每增加10元，就会减少4间客房出租．设每间客房每天的定价增加x元，宾馆出租的客房为y间．求：

(1)、y关于x的函数关系式；

(2)、如果某天宾馆客房收入38400元，那么这天每间客房的价格是多少元？

查看试题解析
23. 如图， $⊙ O$ 的半径 $O D ⊥$ 弦 $A B$ 于点 $C$ ，连结 $A O$ 并延长交 $⊙ O$ 于点 $E$ ，连结 $E C$ .若 $A B = 8$ ， $C D = 2$ ，求 $E C$ 的长.

查看试题解析
24. 如图，在正方形ABCD中，E、F是对角线BD上两点，且∠EAF=45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连接EQ，求证：

(1)、EA是∠QED的平分线；

(2)、EF²=BE²+DF² ．

查看试题解析
25. 如图，抛物线 $y = \frac{1}{2} x^{2} + b x - 2$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于 $C$ 点，且 $A (- 1 ， 0)$ .

(1)、求抛物线的解析式及顶点 $D$ 的坐标；

(2)、判断 $Δ A B C$ 的形状，证明你的结论；

(3)、点 $M$ 是抛物线对称轴上的一个动点，当 $Δ A C M$ 周长最小时，求点 $M$ 的坐标及 $Δ A C M$ 的最小周长.

查看试题解析