山东省德州市武城县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 下列图案中,既是轴对称图形又是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB1C1 , 若AC=2,则图中阴影部分的面积为( )
A、1个 B、2个 C、3个 D、4个2. 如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB1C1 , 若AC=2,则图中阴影部分的面积为( ) A、 B、 C、 D、3. 若二次函数y=x2﹣6x+c的图象过A(﹣1,y1),B(2,y2),C(5,y3),则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1>y3>y2 C、y2>y1>y3 D、y3>y1>y24. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知 ,则球的半径长是( )
A、 B、 C、 D、3. 若二次函数y=x2﹣6x+c的图象过A(﹣1,y1),B(2,y2),C(5,y3),则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1>y3>y2 C、y2>y1>y3 D、y3>y1>y24. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知 ,则球的半径长是( ) A、2 B、2.5 C、3 D、45. 对于二次函数y=x2+2x﹣1的图象与性质,下列说法中正确的是( )A、顶点坐标为(1,2) B、当x<﹣1时,y随x的增大而增大 C、对称轴是直线x=﹣1 D、最小值是﹣16. 已知等腰三角形的三边长分别为 ,且a、b是关于 的一元二次方程 的两根,则 的值是( )A、 B、 C、 或 D、 或7. 将抛物线y=x2+2x+3向下平移3个单位长度后,所得到的抛物线与直线y=3的交点坐标是( )A、(0,3)或(﹣2,3) B、(﹣3,0)或(1,0) C、(3,3)或(﹣1,3) D、(﹣3,3)或(1,3)8. 已知点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )A、
A、2 B、2.5 C、3 D、45. 对于二次函数y=x2+2x﹣1的图象与性质,下列说法中正确的是( )A、顶点坐标为(1,2) B、当x<﹣1时,y随x的增大而增大 C、对称轴是直线x=﹣1 D、最小值是﹣16. 已知等腰三角形的三边长分别为 ,且a、b是关于 的一元二次方程 的两根,则 的值是( )A、 B、 C、 或 D、 或7. 将抛物线y=x2+2x+3向下平移3个单位长度后,所得到的抛物线与直线y=3的交点坐标是( )A、(0,3)或(﹣2,3) B、(﹣3,0)或(1,0) C、(3,3)或(﹣1,3) D、(﹣3,3)或(1,3)8. 已知点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )A、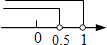 B、
B、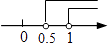 C、
C、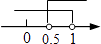 D、
D、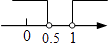 9. 如图,A,B,C,D是⊙O上的四个点,B是 的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
9. 如图,A,B,C,D是⊙O上的四个点,B是 的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( ) A、45° B、60° C、75° D、85°10. 下列说法正确的个数有( )
A、45° B、60° C、75° D、85°10. 下列说法正确的个数有( )①一元二次方程的一般形式为ax2+bx+c=0②平分弦的直径垂直于弦,并且平分弦所对的两条弧.③同弦或等弦所对的圆周角相等④方程x2=x的解是x=1.
A、0 B、1 C、2 D、311. 某商务酒店客房有50间供客户居住.当每间房 每天定价为180元时,酒店会住满;当每间房每天的定价每增加10元时,就会空闲一间房.如果有客户居住,宾馆需对居住的每间房每天支出20元的费用.当房价定为多少元时,酒店当天的利润为10890元?设房价定为x元,根据题意,所列方程是( )A、 B、 C、 D、12. 二次函数 = ( ≠0)图象如图所示,下列结论:① >0;② =0;③当 ≠1时,a+b> ;④ >0;⑤若 = ,且 ≠ ,则 =2.其中正确的有( ) A、①②③ B、②④ C、②⑤ D、②③⑤
A、①②③ B、②④ C、②⑤ D、②③⑤二、填空题
-
13. 已知实数满足(x2﹣x)2﹣(x2﹣x)﹣6=0,则代数式x2﹣x+1= .14. 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=度.
 15. 如图,将⊙O沿弦AB折叠,点C在 上,点D在 上,若∠ACB=70°,则∠ADB=°.
15. 如图,将⊙O沿弦AB折叠,点C在 上,点D在 上,若∠ACB=70°,则∠ADB=°. 16. 设x1、x2是方程x2﹣x﹣2017=0的两实数根,则x12+x1x2+x2﹣2= .17. 如图,直线y1=kx+n(k≠0)与抛物线y2=ax2+bx+c(a≠0)分别交于A(﹣1,0),B(2,﹣3)两点,那么当y1>y2时,x的取值范围是 .
16. 设x1、x2是方程x2﹣x﹣2017=0的两实数根,则x12+x1x2+x2﹣2= .17. 如图,直线y1=kx+n(k≠0)与抛物线y2=ax2+bx+c(a≠0)分别交于A(﹣1,0),B(2,﹣3)两点,那么当y1>y2时,x的取值范围是 . 18. 如图,在直角坐标系中,⊙A的圆心的坐标为(﹣2,0),半径为2,点P为直线y=﹣ x+6上的动点,过点P作⊙A的切线,切点为Q , 则切线长PQ的最小值是 .
18. 如图,在直角坐标系中,⊙A的圆心的坐标为(﹣2,0),半径为2,点P为直线y=﹣ x+6上的动点,过点P作⊙A的切线,切点为Q , 则切线长PQ的最小值是 .
三、解答题
-
19. 已知关于x的方程(1)、求证:方程总有两个实数根(2)、若方程有一个小于1的正根,求实数k的取值范围20. 阅读第(1)题的解题过程,再解答第(2)题:
⑴例:解方程x2﹣|x|﹣2=0.
解:当x≥0时,原方程可化为x2﹣x﹣2=0.
解得:x1=2,x2=﹣1(不合题意.舍去)
当x<0时,原方程可化为x2+x﹣2=0.
解得:x1=﹣2,x2=1(不合题意.舍去)
∴原方程的解是x1=2,x1=﹣2.
⑵请参照上例例题的解法,解方程x2﹣x|x﹣1|﹣1=0.
21. 已知AB是⊙O的的直径,弦CD与AB相交,∠BCD=25°。 (1)、如图1,求∠ABD的大小;(2)、如图2,过点D作O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数。22. 如图,已知:△ABC在正方形网格中.
(1)、如图1,求∠ABD的大小;(2)、如图2,过点D作O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数。22. 如图,已知:△ABC在正方形网格中. (1)、请画出△ABC绕着O逆时针旋转90°后得到的△A1B1C1;(2)、请画出△ABC关于点O对称的△A2B2C2;(3)、在直线MN上求作一点P , 使△PAB的周长最小,请画出△PAB .23. 如图,在等腰三角形PAD中,PA=PD , 以AB为直径的⊙O经过点P , 点C是⊙O上一点,连接AC , PC , PC交AB于点E , 已知∠ACP=60°.
(1)、请画出△ABC绕着O逆时针旋转90°后得到的△A1B1C1;(2)、请画出△ABC关于点O对称的△A2B2C2;(3)、在直线MN上求作一点P , 使△PAB的周长最小,请画出△PAB .23. 如图,在等腰三角形PAD中,PA=PD , 以AB为直径的⊙O经过点P , 点C是⊙O上一点,连接AC , PC , PC交AB于点E , 已知∠ACP=60°. (1)、求证:PD是⊙O的切线;(2)、连接OP , PB , BC , OC , 若⊙O的直径是4,则:
(1)、求证:PD是⊙O的切线;(2)、连接OP , PB , BC , OC , 若⊙O的直径是4,则:①当DE= , 四边形APBC是矩形;
②当DE= , 四边形OPBC是菱形.
24. 如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD , 在AB和BC边各有一个2米宽的小门(不用铁栅栏)设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y . (1)、若所用铁栅栏的长为40米,写出y与x的函数关系式,并求出自变量x的取值范围:(2)、在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?(3)、在(2)的条件下,请直接写出当矩形场地的面积大于192平方米时x的取值范围.25. 如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)、若所用铁栅栏的长为40米,写出y与x的函数关系式,并求出自变量x的取值范围:(2)、在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?(3)、在(2)的条件下,请直接写出当矩形场地的面积大于192平方米时x的取值范围.25. 如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E. (1)、求抛物线的解析式.(2)、点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.(3)、在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.
(1)、求抛物线的解析式.(2)、点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.(3)、在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.