江西省宜春市高安市2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若x＝0是一元二次方程x²+ $\sqrt{b - 1}$ x+b²﹣9＝0的一个根，则b的值是（）

A、9 B、﹣3 C、±3 D、3

查看试题解析
3. 如图，在 $Δ A B C$ 中， $A B = 4$ ， $A C = 3$ ， $∠ B A C = 30 °$ ，将 $Δ A B C$ 绕点 $A$ 按逆时针旋转 $60 °$ 得到 $Δ A B_{1} C_{1}$ ，连接 $B C_{1}$ ，则 $B C_{1}$ 的长为（）

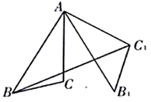A、3 B、4 C、5 D、6

查看试题解析
4. 平移抛物线y＝﹣（x﹣1）（x+3），下列哪种平移方法不能使平移后的抛物线经过原点（）

A、向左平移1个单位 B、向上平移3个单位 C、向右平移3个单位 D、向下平移3个单位

查看试题解析
5. 若关于x的一元二次方程（m+1）x²+2x−1=0有实数根，则m的取值范围是（）

A、m>−2 B、m≥−2 C、m>−2 且 m≠−1 D、m≥−2 且 m≠−1

查看试题解析
6. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，其对称轴为直线x＝﹣1，与x轴的交点为（x₁ ， 0）、（x₂ ， 0），其中0＜x₁＜1，有下列结论：①abc＞0；②﹣3＜x₂＜﹣2；③4a﹣2b+c＜﹣1；④当m为任意实数时，a﹣b＜am²+bm；⑤若点（﹣0.5，y₁），（﹣2，y₂）均在抛物线上，则y₁＞y₂；⑥a＞ $\frac{1}{3}$ ．其中，正确结论的个数为（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

7. 若点 $A (a, 1)$ 与点 $B (- 3 ， b)$ 关于原点对称，则 $a^{b} =$ .

查看试题解析
8. 方程 $x (x + 1) = 2 x + 2$ 的解为．

查看试题解析
9. 如图， $Rt Δ ABC$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，将 $Δ A B C$ ，绕点 $C$ 顺时针旋转 $30 °$ 得到△ $A^{'} B^{'} C^{'}$ ， $C B^{'}$ 与 $A B$ 相交于点 $D$ ，连接 $A A^{'}$ ，则 $∠ B^{'} A^{'} A$ 的度数是 $°$

查看试题解析
10. 《田亩比类乘除捷法》是我国古代数学家杨辉的著作，其中有一个数学问题：“直田积八百六十四步，只云长阔共六十步，问长多阔几何”．意思是：一块矩形田地的面积为864平方步，只知道它的长与宽共60步，问它的长比宽多多少步？根据题意得，长比宽多步．

查看试题解析
11. 若直线 $y = x + m$ 与抛物线 $y = x^{2} - 2 x$ 有交点，则 $m$ 的取值范围是．

查看试题解析
12. 已知函数 $y = (a - 1) x^{2} - 2 a x + a + 2$ 的图象与两坐标轴共有两个交点，则 $a$ 的值为．

查看试题解析

三、解答题

13.

(1)、解方程： $(x - 2) (x + 3) = 6$ ；

(2)、已知抛物线y＝x²+bx+c经过A（﹣1，0）、B（3，0）两点，求该抛物线的顶点坐标．

查看试题解析
14. 已知关于x的一元二次方程x²﹣（2k+1）x+4k﹣3＝0，

(1)、求证：无论k取什么实数值，该方程总有两个不相等的实数根？

(2)、当Rt△ABC的斜边a＝ $\sqrt{31}$ ，且两条直角边的长b和c恰好是这个方程的两个根时，求k的值．

查看试题解析
15. 请仅用无刻度的直尺分别按下列要求画图（保留画图痕迹）．

(1)、如图1，抛物线l与x轴交于A，B两点，与y轴交于点C，CD∥x轴交抛物线于点D，作出抛物线的对称轴EF；

(2)、如图2，抛物线l₁ ， l₂交于点P且关于直线MN对称，两抛物线分别交x轴于点A，B和点C，D，作出直线MN .

查看试题解析
16. 如图，已知△ABC中，AB=AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F.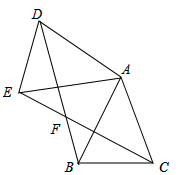

(1)、求证： $Δ A E C ≅ Δ A D B$ ；

(2)、若AB=2， $∠ B A C = 45^{°}$ ，当四边形ADFC是菱形时，求BF的长．

查看试题解析
17. 如图，抛物线 $y = a x^{2} + b x - 2$ 与y轴的交点为A，抛物线的顶点为 $B (1 ， - 3)$ ．

(1)、求出抛物线的解析式；

(2)、点P为x轴上一点，当△PAB的周长最小时，求出点P的坐标．

查看试题解析
18. 在平面直角坐标系中， $Δ A B C$ 的位置如图所示：（每个小方格都是边长为1个单位长度的正方形）

(1)、画出 $Δ A B C$ 关于点 $O$ 的中心对称图形△ $A_{1} B_{1} C_{1}$ ；

(2)、将 $Δ A B C$ 绕着点 $O$ 逆时针旋转 $90 °$ ，画出旋转后得到的△ $A_{2} B_{2} C_{2}$ ；

(3)、请利用格点图，仅用无刻度的直尺画出 $A C$ 边上的高 $B D$ （保留作图痕迹）；

(4)、P为 $y$ 轴上一点，且△PBC是以BC为直角边的直角三角形．请直接写出点P的坐标．

查看试题解析
19. 某服装店销售一批衬衣，每件进价250元，开始以每件400元的价格销售，每星期能卖出20件，后来因库存积压，决定降价销售，经过两次降价后每件售价为324元，每星期能卖出172件．

(1)、已知两次降价的百分率相同，求每次降价的百分率；

(2)、喜欢研究数学的店长在降价的过程中发现，适当的降价可增加销售又可增加收入，且每件衬衣售价每降低1元，销售量会增加2件，若店长想要每星期获利11000元，为了让顾客得到更大的实惠，应把售价定为多少元？

查看试题解析
20. 若二次函数y＝kx²+（3k+2）x+2k+2．

(1)、求证：抛物线与x轴有交点．

(2)、经研究发现，无论k为何值，抛物线经过某些特定的点，请求出这些定点．

(3)、若y₁＝2x+2，在﹣2＜x＜﹣1范围内，请比较y₁ ， y的大小．

查看试题解析
21. 某数学兴趣小组在探究函数 $y = x^{2} - 2 | x | + 3$ 的图象和性质时，经历了以下探究过程：

(1)、列表如下：

写出表中m、n的值：m＝，n＝；

(2)、描点并在图中画出函数的大致图象；

(3)、根据函数图象，完成以下问题：
①观察函数 $y = x^{2} - 2 | x | + 3$ 的图象，以下说法正确的有（填写正确的序号）

A．对称轴是直线x＝1；

B．函数 $y = x^{2} - 2 | x | + 3$ 的图象有两个最低点，其坐标分别是（﹣1，2）、（1，2）；

C．当﹣1＜x＜1时，y随x的增大而增大；

D．当函数 $y = x^{2} - 2 | x | + 3$ 的图象向下平移3个单位时，图象与x轴有三个公共点；

E．函数 $y = {(x - 2)}^{2} - 2 | x - 2 | + 3$ 的图象，可以看作是函数 $y = x^{2} - 2 | x | + 3$ 的图象向右平移2个单位得到．

②结合图象探究发现，当m满足时，方程 $x^{2} - 2 | x | + 3 = m$ 有四个解．

③设函数 $y = x^{2} - 2 | x | + 3$ 的图象与其对称轴相交于P点，当直线y＝n和函数 $y = x^{2} - 2 | x | + 3$ 图象只有两个交点时，且这两个交点与点P所构成的三角形是等腰直角三角形，则n的值为．

查看试题解析
22. 如图

(1)、如图①，在等边三角形ABC内，点P到顶点A，B，C的距离分别是3，4，5，则∠APB= ，由于 $P A$ ，PB，PC不在同一三角形中，为了解决本题，我们可以将△ABP绕点A逆时针旋转60^o到 $△ A C P'$ 处，连接 $P P'$ ，此时， $Δ A C P'$ ≌ ，就可以利用全等的知识，进而将三条线段的长度转化到一个三角形中，从而求出∠APB的度数；

(2)、请你利用第（1）题的解答方法解答：如图②，△ABC中， $∠ C A B = 90^{°} ， A B = A C$ ，D、E为BC上的点，且 $∠ D A E = 45^{o}$ ，求证： $B D^{2} + E C^{2} = D E^{2}$ ；

(3)、如图③，在△ABC中， $∠ C A B = 120^{°} ， A B = A C ， ∠ E A D = 60^{°} ， B C = 3 + \sqrt{3}$ ，若以BD、DE、EC为边的三角形是直角三角形时，求BE的长．

查看试题解析
23. 二次函数y＝a（x﹣h）²+k（a≠0）的图象是抛物线，定义一种变换，先作这条抛物线关于原点对称的抛物线y′，再将得到的对称抛物线y′向上平移m（m＞0）个单位，得到新的抛物线y_m ，我们称y_m叫做二次函数y＝a（x﹣h）²+k（a≠0）的m阶变换．

(1)、已知：二次函数y＝2（x+2）²+1，它的顶点关于原点的对称点为，这个抛物线的2阶变换的表达式为．

(2)、若二次函数M的6阶变换的关系式为y₆′＝（x﹣1）²+5．
①二次函数M的函数表达式为．

②若二次函数M的顶点为点A ，与x轴相交的两个交点中左侧交点为点B ，在抛物线y₆′＝（x﹣1）²+5上是否存在点P ，使点P与直线AB的距离最短，若存在，求出此时点P的坐标．

(3)、抛物线y＝﹣3x²﹣6x+1的顶点为点A ，与y轴交于点B ，该抛物线的m阶变换的顶点为点C．若△ABC是以AB为腰的等腰三角形，请直按写出m的值．

查看试题解析