江苏省苏州市张家港市2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 流感病毒的直径约为0.00000072m，其中0.00000072用科学记数法可表示为（）

A、7.2×10⁷ B、7.2×10^-8 C、7.2×10^-7 D、0.72×10^-8

查看试题解析
2. 计算（a²）²的结果是（）

A、a⁴ B、a⁵ C、a⁶ D、a⁸

查看试题解析
3. 下列各组数据中，能构成三角形的是（）

A、1，2，3 B、2，3，4 C、4，9，4 D、2，1，4

查看试题解析
4. 不等式x﹣2≤0的解集在以下数轴表示中正确的是（）

A、 B、 C、 D、

查看试题解析
5. 如果 $\frac{1}{5} a^{2} b^{2}$ 与 $- \frac{1}{4} a^{x + 1} b^{4 x - y}$ 是同类项，则x、y的值分别是（）

A、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$

查看试题解析
6. 一个多边形的内角和等于 $1260 °$ ，则它是（）边形

A、7 B、8 C、9 D、10

查看试题解析
7. 下列命题是真命题的是（）

A、内错角相等 B、如果a²＝b² ，那么a＝b C、三角形的一个外角大于任何一个内角 D、平行于同一直线的两条直线平行

查看试题解析
8. 已知 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ 是二元一次方程组 ${\begin{array}{l} 3 x + 2 y = m \\ m x - y = n \end{array}$ 的解，则m﹣n的值为（）

A、1 B、2 C、3 D、4

查看试题解析
9. 若关于x的不等式组 ${\begin{array}{l} x - m < 0 \\ 3 - 2 x ⩽ 1 \end{array}$ 所有整数解的和是6，则m的取值范围是（）

A、2＜m≤3 B、2≤m＜3 C、3＜m≤4 D、3≤m＜4

查看试题解析
10. 如图，大正方形的边长为m，小正方形的边长为n，若用x，y表示四个长方形的两边长（x＞y），观察图案及以下关系式：① $x - y = n$ ；② $x y = \frac{m^{2} - n^{2}}{2}$ ；③ $x^{2} - y^{2} = m n$ ；④ $x^{2} + y^{2} = \frac{m^{2} + n^{2}}{2}$ .其中正确的关系式有（）

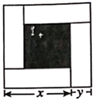A、①② B、①③ C、①③④ D、①②③④

查看试题解析

二、填空题

11. 计算 $x^{6} \div x^{2} =$ .

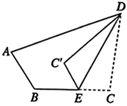
查看试题解析
12. 在二元一次方程2x﹣y＝1中，若x＝﹣4，则y＝.

查看试题解析
13. 不等式组 ${\begin{array}{l} \frac{x + 5}{2} > 1 \\ 4 - x \geq 1 \end{array}$ 的解集是.

查看试题解析
14. 计算 $(x + a) (2 x - 1)$ 的结果中不含关于字母x的一次项，则a=.

查看试题解析
15. 若a^x＝2，a^y＝3，则a^2x^﹣^y＝.

查看试题解析
16. 已知x，y满足二元一次方程2x﹣y＝1，若3y＋1＜0，则x的取值范围是.

查看试题解析
17. 已知 $a + b = 2$ ，则 $a^{2} - b^{2} + 2 a + 6 b + 2$ 的值为.

查看试题解析
18. 如图，在四边形ABCD中，∠B＝120°，∠B与∠ADC互为补角，点E在BC上，将△DCE沿DE翻折，得到△DC′E，若AB∥C′E，DC′平分∠ADE，则∠A的度数为°.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(- 2)}^{2} + 6 \times 2^{- 1} - {(π - 1)}^{0}$ ；

(2)、 $(a + 3) (a - 1) - (a + 2) (a - 2)$ .

查看试题解析
20. 分解因式：

(1)、 $4 x^{2} - 36$ ；

(2)、 ${(x - 2)}^{2} - 2 x + 4$ .

查看试题解析
21. 解方程组 ${\begin{matrix} x - y = 8 \\ 3 x + y = 12 \end{matrix}$ ．

查看试题解析
22. 解不等式： $\frac{2 x - 1}{3} - \frac{9 x + 2}{6} \geq 1$ ，并把解集表示在数轴上.

查看试题解析
23. 已知 $x + y = 4$ ， $x^{2} + y^{2} = 10$ .

(1)、求xy的值；

(2)、求 ${(x - y)}^{2} - 3$ 的值.

查看试题解析
24. 如图， $∠ A = 64 ° ， ∠ B = 76 °$ ，将纸片的一角折叠，使点 $C$ 落在 $Δ A B C$ 外，若 $∠ A E C^{'} = 22 °$ ，求 $∠ B D C^{'}$ 的度数.

查看试题解析
25. 已知关于x、y的方程组 ${\begin{array}{l} x + y = m - 9 \\ 3 x - 2 y = 8 m - 2 \end{array}$ .

(1)、求方程组的解（用含m的代数式表示）；

(2)、若方程组的解满足x≤0，y＜0，且m是正整数，求m的值.

查看试题解析
26. 如图，已知∠BDC＋∠EFC＝180°，∠DEF＝∠B.

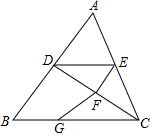(1)、求证：ED∥BC；

(2)、若D，E，F分别是AB，AC，CD边上的中点，四边形ADFE的面积为6.
①求△ABC的面积；
②若G是BC边上一点，CG＝2BG，求△FCG的面积.

查看试题解析
27. 共享经济来临，某企业决定在无锡投入共享单车（自行车）和共享电单车（电动车）共2000辆，已知每辆共享单车成本380元，每台共享电单车成本1500元，2辆共享单车和1辆共享电单车每周毛利31元，4辆共享单车和3辆共享电单车每周毛利81元，

(1)、求共享单车和共享电单车每周每辆分别可以盈利多少元？

(2)、为考虑投资回报率，该企业计划投入成本不超过174万元，每周的毛利不低于23050元，现要求投入的单车数量为10的倍数，请你列举出所有投入资金方案.

查看试题解析
28. 在△ABC中，∠BAC＝90°，点D是BC上一点，将△ABD沿AD翻折后得到△AED，边AE交射线BC于点F.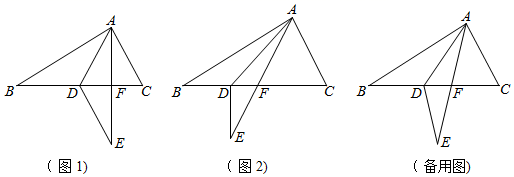

(1)、如（图1），当AE⊥BC时，求证：DE∥AC

(2)、若∠C＝2∠B，∠BAD＝x°（0＜x＜60）
①如（图2），当DE⊥BC时，求x的值.

②是否存在这样的x的值，使得△DEF中有两个角相等.若存在，并求x的值；若不存在，请说明理由.

查看试题解析