江西省南昌市新建区2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. $x = 2$ 满足下列方程的是（）

A、 $x^{2} = 2$ B、 $x^{2} = 4$ C、 $x^{2} = 8$ D、 $x^{2} = 16$

查看试题解析
2. 下列四个图中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如果将抛物线 $y = 2 x^{2}$ 向上平移2个单位，那么所得新抛物线的表达式是 $($ $)$

A、 $y = 2 x^{2} + 1$ B、 $y = {(2 x + 2)}^{2}$ C、 $y = 2 x^{2} + 2$ D、 $y = {(2 x + 1)}^{2}$

查看试题解析
4. 关于二次函数 $y = x^{2} - 4 x - 4$ 的说法，正确的是（）

A、最大值为-4 B、最小值为-4 C、最大值为-8 D、最小值为-8

查看试题解析
5. 不解方程，判断下列一元二次方程中，一定有实数根的是（）

A、 $x^{2} - x + 4 = 0$ B、 $- x^{2} + x - 2 = 0$ C、 $x^{2} - 4 x - 2019 = 0$ D、 $x^{2} - x + 2020 = 0$

查看试题解析
6. 某种植基地2016年蔬菜产量为80吨，预计2018年蔬菜产量达到100吨，求蔬菜产量的年平均增长率，设蔬菜产量的年平均增长率为x，则可列方程为（）

A、80（1+x）²=100 B、100（1﹣x）²=80 C、80（1+2x）=100 D、80（1+x²）=100

查看试题解析
7. 若 $m$ ， $n$ 是方程 $x^{2} - 2 x - 5 = 0$ 两根，则 $(m^{2} - 2 m) (m + n)$ 的值为（）

A、5 B、10 C、-5 D、-10

查看试题解析
8. 对于二次函数 $y = a x^{2} - 2 a x + 3 (a \neq 0)$ ，下列说法错误的是（）

A、对称轴为直线 $x = 1$ B、一定经过点 $(2 ， 3)$ C、当 $x < 1$ 时， $y$ 随 $x$ 增大而增大 D、当 $a > 0$ ， $m \neq 1$ 时， $a m^{2} - 2 a m + 3 > - a + 3$ .

查看试题解析

二、填空题

9. 点 $P (- 3, 4)$ 关于原点的对称点的坐标为.

查看试题解析
10. 二次函数 $y = {(x + 2)}^{2} - 3$ 的顶点坐标是.

查看试题解析
11. 若 $α$ ， $β$ 分别是方程 $x^{2} - 3 x - 6 = 0$ 的两实根，则 $\frac{α β}{α + β}$ 的值是.

查看试题解析
12. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ B = 70 °$ ，把 $Δ A B C$ 绕点 $C$ 顺时针旋转得到 $Δ E D C$ ，若点 $B$ 恰好落在 $A B$ 边上 $D$ 处，则 $∠ 1 =$ °.

查看试题解析
13. 如图是抛物线 $y = a x^{2} + b x + c$ 的一部分，另一部分被墨水污染，发现：对称轴为直线 $x = 1$ ，与 $x$ 轴的一个交点为 $(3 ， 0)$ ，请你经过推理分析，不等式 $a x^{2} + b x + c > 0$ 的解集是.

查看试题解析
14. 用两块完全相同的直角三角形纸片，拼成一个四边形，若直角三角形两直角边分别为3，4，则拼成的四边形中，较长的对角线的长度可能为.

查看试题解析

三、解答题

15.

(1)、 $x^{2} - 4 x - 1 = 0$ （配方法）；

(2)、 $2 x^{2} - 3 x - 1 = 0$ （公式法）；

(3)、 $x (x - 2) - 3 x + 6 = 0$ （因式分解法）.

查看试题解析
16. 已知关于 $x$ 的方程 $x^{2} - 2 x + 2 k - 1 = 0$ 有实数根.

(1)、求 $k$ 的取值范围.

(2)、设方程的两根分别是 $x_{1}$ ， $x_{2}$ ，且满足 ${(x_{1} \cdot x_{2})}^{2} - {(x_{1} + x_{2})}^{2} = 0$ ，试求 $k$ 的值.

查看试题解析
17. 已知抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴交于 $A$ ， $B$ ，与 $y$ 轴交下点 $C$ ，请仅用无刻度直尺按要求作图：

(1)、在图1中，直线 $l$ 为对称轴，请画出点 $C$ 关于直线 $l$ 的对称点；

(2)、在图2中，若 $C D ∥ x$ 轴，请画出抛物线的对称轴.

查看试题解析
18. 如图，有一块矩形硬纸板，长 $30 c m$ ，宽 $20 c m$ .在其四角各剪去一个同样的正方形，然后将四周突出部分折起，可制成一个无盖长方体盒子.当剪去正方形的边长取何值时，所得长方体盒子的侧面积为 $200 c m^{2}$ ？

查看试题解析
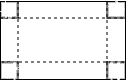19. 在Rt△ABC中，∠ABC=90°，∠BAC＝30°，将△ABC绕点A顺时针旋转一定的角度 $α$ 得到△AED ，点B、C的对应点分别是E、D.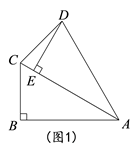

(1)、如图1，当点E恰好在AC上时，求∠CDE的度数；

(2)、如图2，若 $α$ =60°时，点F是边AC中点，求证：四边形BFDE是平行四边形.

查看试题解析

20. “互联网+”时代，网上购物备受消费者青睐，某网店专售一款休闲裤，其成本为每条40元，据市场调查发现每月的销售量与售价的关系如下表：

售价 $x$ （元）	…	50	60	70	80	…
销售量 $y$ （条）	…	250	200	150	100	…

(1)、设每条裤子的售价为

x

元（

x

为正整数），每月的销售量为

y

条.直接写出

y

与

x

的函数关系式（不要求写

x

的取值范围）；

(2)、若每月利润为4000元，且让消费者得到最大的实惠，则定价多少元？

(3)、设该网店每月获得的利润为

w

元，当销售单价定价多少元时，每月获得的利润最大，最大利润是多少？

查看试题解析

21. 抛物线 $C_{1}$ ： $y_{1} = a_{1} x^{2} + b_{1} x + c$ 与抛物线 $C_{2}$ ： $y_{2} = a_{2} x^{2} + b_{2} x + c$ 中，若 $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}$ ，则称抛物线 $C_{1}$ ， $C_{2}$ 为“窗帘”抛物线.

(1)、已知 $y = x^{2} + 2 x - 3$ 与 $y = 2 x^{2} + b x - 3$ 是“窗帘”抛物线，
① $b$ 的值为；

②在如图的坐标系中画出它们的大致图像，并直接写出它们的交点坐标.

(2)、设抛物线 $y = x^{2} + 2 x - 3$ ， $y = n x^{2} + 2 n x - 3$ ， $y = 3 n x^{2} + 6 n x - 3$ $(n > 0)$ 的顶点分别为 $D$ ， $E$ ， $F$ ，
①判断它们是否是“窗帘”抛物线？答：（填“是”或“不是”）

②若 $E F = 3 D E$ ，求 $n$ 的值.

查看试题解析