江西省南昌市二十八中教育集团2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 把一元二次方程x（x+1）＝3x+2化为一般形式，正确的是（）

A、x²+4x+3＝0 B、x²﹣2x+2＝0 C、x²﹣3x﹣1＝0 D、x²﹣2x﹣2＝0

查看试题解析
2. 抛物线y＝﹣（x+3）² ﹣7的对称轴是（）

A、y轴 B、直线x＝3 C、直线x＝﹣3 D、直线x＝﹣7

查看试题解析
3. 抛物线 $y = - 2 x^{2}$ 向左平移2个单位，再向下平移3个单位，得到的抛物线解析式为（）

A、 $y = - 2 {(x - 2)}^{2} - 3$ B、 $y = - 2 {(x + 2)}^{2} - 3$ C、 $y = 2 {(x - 2)}^{2} - 3$ D、 $y = 2 {(x + 2)}^{2} - 3$

查看试题解析
4. 如图是二次函数 $y = - x^{2} + 2 x + 4$ 的图象，使 $y ⩾ 1$ 成立的x的取值范围是（）

A、 $- 1 ⩽ x ⩽ 3$ B、 $x ⩽ - 1$ C、 $x ⩾ 1$ D、 $x ⩽ - 1$ 或 $x ⩾ 3$

查看试题解析
5. 已知二次函数y＝ax²+bx+c（a≠0）的图象如图所示，有下列结论：①b²﹣4ac＞0；②abc＞0；③a+c＞0；④9a+3b+c＜0．其中，正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. 如图， $Rt △ O A B$ 的顶点 $A (- 2 ， 4)$ 在抛物线 $y = a x^{2}$ 上，将 $Rt △ O A B$ 绕点 $O$ 顺时针旋转 $90 °$ ，得到 $△ O C D$ ，边 $C D$ 与该抛物线交于点 $P$ ，则点 $P$ 的坐标为（）．

A、 $(\sqrt{2} ， \sqrt{2})$ B、 $(2 ， 2)$ C、 $(\sqrt{2} ， 2)$ D、 $(2 ， \sqrt{2})$

查看试题解析

二、填空题

7. 已知x＝﹣1是一元二次方程x²﹣2mx+1＝0的一个解，则m的值是．

查看试题解析
8. 若点（2，﹣5）、（6，﹣5）在抛物线y＝ax²+bx+c上，则它的对称轴是．

查看试题解析
9. 若点（a，1）与（﹣2，b）关于原点对称，则a^b= ．

查看试题解析
10. 烟花厂为国庆70周年庆祝晚会特别设计制作一种新型礼炮，这种礼炮的升空高h（m）与飞行时间t（s）的关系式是 $h = \frac{5}{2} t^{2} + 20 t + 1$ ，若这种礼炮在点火升空到最高点处引爆，则从点火升空到引爆需要时间为.

查看试题解析
11. 如图，等腰 $Rt Δ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C = 1$ ，且AC边在直线a上，将 $Δ A B C$ 绕点A顺时针旋转到位置①可得到点 $P_{1}$ ，此时 $A P_{l} = \sqrt{2}$ ；将位置①的三角形绕点 $P_{1}$ 顺时针旋转到位置②，可得到点 $P_{2}$ ，此时 $A P_{2} = 1 + \sqrt{2}$ ；将位置②的三角形绕点 $P_{2}$ 顺时针旋转到位置③，可得到点 $P_{3}$ ，此时 $A P_{3} =$ ， …，按此规律继续旋转，直至得到点 $P_{2019}$ 为止，则 $A P_{2019} =$ .

查看试题解析
12. 若抛物线 $y = x^{2} - b x + 9$ 的顶点在坐标轴上，则b的值为.

查看试题解析

三、解答题

13. x²+4x﹣2＝0．

查看试题解析
14. 4x²﹣3=12x（用公式法解）

查看试题解析
15. 解方程：2(x－3)＝3x(x－3)．

查看试题解析
16. 解方程： $x^{2} - 3 x + 2 = 0$ .

查看试题解析
17. 关于x的一元二次方程x²+（2m﹣1）x+m²＝0有实数根．

(1)、求m的取值范围；

(2)、若两根为x₁、x₂且x₁²+x₂²＝7，求m的值．

查看试题解析
18. 已知二次函数y＝a(x﹣1)²+4的图象经过点(﹣1，0)．

(1)、求这个二次函数的解析式；

(2)、判断这个二次函数的开口方向，对称轴和顶点坐标．

查看试题解析
19. 习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气”．某校为响应我市全民阅读活动，利用节假日面向社会开放学校图书馆．据统计，第一个月进馆 $128$ 人次，进馆人次逐月增加，到第三个月末累计进馆 $608$ 人次，若进馆人次的月平均增长率相同．

(1)、求进馆人次的月平均增长率；

(2)、因条件限制，学校图书馆每月接纳能力不超过 $500$ 人次，在进馆人次的月平均增长率不变的条件下，校图书馆能否接纳第四个月的进馆人次，并说明理由．

查看试题解析
20. 如图，E是正方形ABCD申CD边上任意一点．

(1)、以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形；

(2)、在BC边上画一点F，使△CFE的周长等于正方形ABCD的周长的一半，请简要说明你取该点的理由．

查看试题解析
21. 如图，隧道的截面由抛物线和长方形构成，长方形的长为16m，宽为6m，抛物线的最高点C离地面AA₁的距离为8m．

(1)、按如图所示的直角坐标系，求表示该抛物线的函数表达式．

(2)、一大型汽车装载某大型设备后，高为7m，宽为4m，如果该隧道内设双向行车道，那么这辆贷车能否安全通过？

查看试题解析
22. 如图，△ABC中，∠C=90°，BC=6cm，AC=8cm，点P从点A开始沿AC向点C以2厘米/秒的速度运动；与此同时，点Q从点C开始沿CB边向点B以1厘米/秒的速度运动；如果P、Q分别从A、C同时出发，当其中一点到达终点时，另一点也随之停止运动．

(1)、经过几秒，△CPQ的面积等于3cm²？

(2)、在整个运动过程中，是否存在某一时刻t，使PQ恰好平分△ABC的面积？若存在，求出运动时间t；若不存在，请说明理由．

(3)、是否存在某一时刻，PQ长为 $\sqrt{29}$ ，如果存在，求出运动时间t。

查看试题解析
23. 某商店经销甲、乙两种商品，已知一件甲种商品和一件乙种商品的进价之和为30元，每件甲种商品的利润是4元，每件乙种商品的售价比其进价的2倍少11元，小明在该商店购买8件甲种商品和6件乙种商品一共用了262元.

(1)、求甲、乙两种商品的进价分别是多少元；

(2)、在（1）的前提下，经销商统计发现，平均每天可售出甲种商品400件和乙种商品300件，如果将甲种商品的售价每提高0.1元，则每天将少售出7件甲种商品；如果将乙种商品的售价每提高0.1元，则每天将少售出8件乙种商品，经销商决定把两商品的价格都提高a元，在不考虑其他因素的条件下，当a为多少时，才能使该经销商每天销售甲、乙两种商品获取的利润共2500元.

查看试题解析
24. 如图1，在 $R t Δ A B C$ 中， $∠ A = 90 °$ ， $A B = A C$ ，点 $D$ 、 $E$ 分别在边 $A B$ 、 $A C$ 上， $A D = A E$ ，连结 $D C$ ，点 $M$ 、 $P$ 、 $N$ 分别为 $D E$ 、 $D C$ 、 $B C$ 的中点.

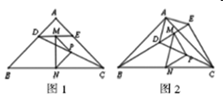(1)、观察猜想图1中，线段 $P M$ 与 $P N$ 的数量关系是，位置关系是；

(2)、探究证明把 $Δ A D E$ 绕点 $A$ 逆时针方向旋转到图2的位置，连结 $M N$ 、 $B D$ 、 $C E$ ，判断 $Δ P M N$ 的形状，并说明理由；

(3)、拓展延伸把 $Δ A D E$ 绕点 $A$ 在平面内自由旋转，若 $A D = 4$ ， $A B = 10$ ，请直接写出 $Δ P M N$ 面积的最大值.

查看试题解析
25. 如图①，已知抛物线 $y = a x^{2} + b x + 3$ （a≠0）与 $x$ 轴交于点A（1，0）和点B（－3，0），与y轴交于点C．

(1)、求抛物线的解析式；

(2)、设抛物线的对称轴与 $x$ 轴交于点M，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

(3)、如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．

查看试题解析