江西省吉安市七校联盟2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 关于一元二次方程x²﹣2x+1﹣a＝0无实根，则a的取值范围是（）

A、a＜0 B、a＞0 C、a＜ $\frac{3}{4}$ D、a＞ $\frac{3}{4}$

查看试题解析
2. 已知：如图，小华在打羽毛球时，扣球要使球恰好能打过网，而且落在离网前4米的位置处，则球拍击球的高度h应为（）

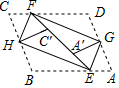
A、1.55m B、3.1m C、3.55m D、4m

查看试题解析
3. 在一个不透明的布袋中，有红色、黑色、白色球共40个，它们除颜色外其他完全相同，小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在 $15 %$ 和 $45 %$ ，则布袋中白色球的个数可能是（）

A、24 B、18 C、16 D、6

查看试题解析
4. 某商品原价为200元，连续两次降价x%后，售价为148元．下面所列方程正确的是（）

A、200（1﹣x%）²＝148 B、200（1+x%）²＝148 C、200（1﹣2x%）＝148 D、200（1﹣x²%）＝148

查看试题解析
5. 我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.已知四边形ABCD的中点四边形是正方形，对角线AC与BD的关系，下列说法正确的是（）

A、AC，BD相等且互相平分 B、AC，BD垂直且互相平分 C、AC，BD相等且互相垂直 D、AC，BD垂直且平分对角

查看试题解析
6. 如图，在 $Rt Δ A B C$ 中， $A B = A C$ ， $D$ 、 $E$ 是斜边 $B C$ 上两点，且 $∠ D A E = 45 °$ ，将 $Δ A D C$ 绕点 $A$ 顺时针旋转 $90 °$ 后，得到 $Δ A F B$ ，连结 $E F$ ，下列结论：① $Δ A E D ≌ Δ A E F$ ；② $Δ A B E ≌ Δ A C D$ ；③ $B E + D C = D E$ ；④ $B E^{2} + D C^{2} = D E^{2}$ .其中正确的是（）.

A、②④ B、①④ C、②③ D、①③

查看试题解析

二、填空题

7. 小明用0﹣9中的数字给手机设置了六位开机密码，但他把最后一位数字忘记了，小明只输入一次密码就能打开手机的概率是.

查看试题解析
8. 菱形有一个内角为60°，较短的对角线长为6，则它的面积为．

查看试题解析
9. 要使 $\frac{m^{2} - 2 m - 3}{m + 1}$ 的值为零，则m＝．

查看试题解析
10. 已知x₁ ， x₂是方程x²﹣x﹣3＝0的两根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ ＝．

查看试题解析
11. 如图，平行四边形纸片ABCD的边AB，BC的长分别是10cm和7.5cm，将其四个角向内对折后，点B与点C重合于点C'，点A与点D重合于点A′.四条折痕围成一个“信封四边形”EHFG，其顶点分别在平行四边形ABCD的四条边上，则EF＝cm.

查看试题解析
12. 在方格纸中，每个小格的顶点称为格点，以格点的连线为边的三角形称为格点三角形，如图所示的5×5的方格纸中，如果想作格点△ABC与△OAB相似（相似比不能为1），则C点坐标为．

查看试题解析

三、解答题

13. 用适当的方法解方程．

(1)、2x²﹣6x+1＝0；

(2)、9（x﹣2）²＝4 （2x+5）² ．

查看试题解析
14.
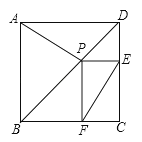
已知：P是正方形ABCD对角线BD上一点，PE⊥DC，PF⊥BC，E、F分别为垂足．
求证：AP=EF．

查看试题解析
15.
如图，六个完全相同的小长方形拼成了一个大长方形，AB是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．

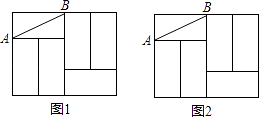(1)、在图1中画出一个45°角，使点A或点B是这个角的顶点，且AB为这个角的一边；

(2)、在图2中画出线段AB的垂直平分线．

查看试题解析
16. 为纪念建国70周年，某校举行班级歌咏比赛，歌曲有：《我爱你，中国》，《歌唱祖国》，《我和我的祖国》（分别用字母A，B，C依次表示这三首歌曲）．比赛时，将A，B，C这三个字母分别写在3张无差别不透明的卡片正面上，洗匀后正面向下放在桌面上，八（1）班班长先从中随机抽取一张卡片，放回后洗匀，再由八（2）班班长从中随机抽取一张卡片，进行歌咏比赛．

(1)、八（1）班抽中歌曲《我和我的祖国》的概率是；

(2)、试用画树状图或列表的方法表示所有可能的结果，并求出八（1）班和八（2）班抽中不同歌曲的概率．

查看试题解析
17. 如图，已知点D是 $△ ABC$ 的边AC上的一点，连接 $BD . ∠ ABD = ∠ C$ ， $AB = 6$ ， $AD = 4$ .

(1)、求证： $△ ABD$ ∽ $△ ACB$ ；

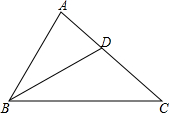(2)、求线段CD的长.

查看试题解析
18. 一个不透明的袋中装有5个黄球、13个黑球和22个红球，它们除颜色外都相同．

(1)、求从袋中摸出一个球是黄球的概率；

(2)、现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后，使从袋中摸出一个球是黄球的概率不小于 $\frac{1}{3}$ ，问至少取出了多少个黑球？

查看试题解析
19. 如图，在△ABC中，AB=AC，AD ⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE ⊥AN，垂足为点E．

(1)、求证：四边形ADCE为矩形；

(2)、当△ABC满足什么条件时，四边形ADCE是一个正方形?并给出证明．

查看试题解析
20. 如图，在△ABC中，∠B＝90°，AB＝12mm，BC＝24mm，动点P以2mm/s的速度从A向B移动，（不与B重合），动点Q以4mm/s的速度从B向C移动，（不与C重合），若P、Q同时出发，试问：

(1)、经过几秒后，△PBQ与△ABC相似．

(2)、经过几秒后，四边形APQC的面积最小？并求出最小值．

查看试题解析
21. 一家化工厂原来每月利润为120万元，从今年1月起安装使用回收净化设备（安装时间不计），一方面改善了环境，另一方面大大降低原料成本.据测算，使用回收净化设备后的1至x月（1≤x≤12）的利润的月平均值w（万元）满足w=10x+90,第二年的月利润稳定在第1年的第12个月的水平．

(1)、设使用回收净化设备后的1至x月（1≤x≤12）的利润和为y,写出y关于x的函数关系式，并求前几个月的利润和等于700万元？

(2)、当x为何值时，使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等？

(3)、求使用回收净化设备后两年的利润总和．

查看试题解析
22. 如图，在△ABD中，AB=AD，AO平分∠BAD，过点D作AB的平行线交AO的延长线于点C，连接BC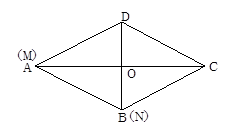

(1)、求证：四边形ABCD是菱形．

(2)、如果OA，OB(OA>OB)的长（单位：米）是一元二次方程 $x^{2} - 7 x + 12 = 0$ 的两根，求AB的长以及菱形ABCD的面积．

(3)、若动点M从A出发，沿AC以2m/S的速度匀速直线运动到点C，动点N从B 出发，沿BD以1m/S的速度匀速直线运动到点D，当M运动到C点时运动停止．若M、N同时出发，问出发几秒钟后，△MON的面积为 $\frac{1}{4} m^{2}$ ？

查看试题解析
23. 如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角扳的一边交CD于点F，另一边交CB的延长线于点G，

(1)、求证：EF=EG；

(2)、如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：

(3)、如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB=a、BC=b，求 $\frac{E F}{E G}$ 的值．

查看试题解析