江西省赣州市章贡区2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 抛物线y＝（x﹣1）²+3的顶点坐标是（）

A、（1，3） B、（﹣1，3） C、（1，﹣3） D、（3，﹣1）

查看试题解析
2. 下列汽车标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 一元二次方程 $(x + 1) (x - 1) = 2 x + 3$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
4. 如图，一块含30°角的直角三角板ABC绕点C顺时针旋转到△ABC ，当B，C，A在一条直线上时，三角板ABC的旋转角度为（）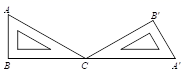

A、30° B、60° C、120° D、150°

查看试题解析
5. 如图，在⊙O中， $\overset{⌢}{A B}$ 所对的圆周角∠ACB＝55°，若P为 $\overset{⌢}{A B}$ 上一点，∠AOP＝73°，OP∥CB ，则∠OBC的度数为（）

A、30° B、35° C、37° D、55°

查看试题解析
6. 抛物线y＝ax²+bx+c的顶点为(﹣1，3)，与x轴的交点A在点(﹣3，0)和(﹣2，0)之间，其部分图象如图，则以下结论，其中符合题意结论的个数为（）
①若点P(﹣3，m)，Q(3，n)在抛物线上，则m＜n；②c＝a+3；③a+b+c＜0；④方程ax²+bx+c＝3有两个相等的实数根．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 关于x的一元二次方程2x²﹣x﹣k＝0的一个根为1，则k的值是．

查看试题解析
8. 在平面直角坐标系中，点A的坐标为（a，3），点B的坐标是（4，b），若点A与点B关于原点O对称，则ab= ．

查看试题解析
9. 在平面直角坐标系中，⊙P的圆心坐标为（4，8），半径为5，那么x轴与⊙P的位置关系是．

查看试题解析
10. 若抛物线y=x²与直线y=x+2的交点坐标为（﹣1，1）和（2，4），则方程x²﹣x﹣2=0的解为．

查看试题解析
11. 如图，AB是半圆O的直径，AC为弦，OD⊥AC于D，过点O作OE∥AC交半圆O于点E，过点E作EF⊥AB于F．若AC=2，则OF的长为．

查看试题解析
12. 如图，P是抛物线y＝x²﹣4x+3上的一点，以点P为圆心、1个单位长度为半径作⊙P，当⊙P与直线y＝0相切时，点P的坐标为．

查看试题解析

三、解答题

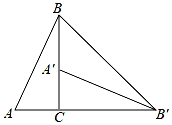
13. 解方程：3（x﹣2）＝5x（x﹣2）

查看试题解析
14. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A'B'C ，连接BB'，若∠A'B'B＝20°，求∠A的度数．

查看试题解析
15. 如图，已知点E在直角三角形ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D ．

(1)、请仅用无刻度的直尺在图1中作出∠BAC的平分线；

(2)、请仅用无刻度的直尺在图2中的线段BC上取一个点P ，使CP＝EF ．

查看试题解析
16. 在平面直角坐标系中xOy中，抛物线y＝ax²﹣4ax+1．

(1)、求抛物线的对称轴；

(2)、若抛物线过点A（﹣1，6），求二次函数的表达式；

(3)、若抛物线与坐标轴只有两个交点，求a的值．

查看试题解析
17. 在我国古代数学著作《九章算术》中记载了这样一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用现代语言表述为：如图，AB为⊙O的直径，弦CD⊥AB于点E，AE＝1寸，CD＝10寸，求直径AB的长.请你解答这个问题.

查看试题解析
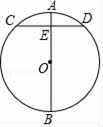18. 将两块全等的含30°角的直角三角板按如图1所示的方式放置，已知∠BAC＝∠B₁A₁C＝30°．固定三角板A₁B₁C ，然后将三角板ABC绕直角顶点C顺时针旋转（旋转角小于90°）至如图2所示的位置，AB与A₁C、A₁B₁分别交于点D、E ， AC与A₁B₁交于点F ．

(1)、当旋转角等于20°时，∠BCB₁＝°；

(2)、当旋转角等于多少度时，AB与A₁B₁垂直？请说明理由．

查看试题解析
19. 已知关于x的一元二次方程x²﹣2（k﹣1）x+k²﹣k﹣2＝0有两个不相等的实数根x₁ ， x₂ ．

(1)、求k的取值范围；

(2)、若x₁ ， x₂满足x₁²+x₂²﹣x₁x₂＝24，求k的值．

查看试题解析
20. 赣县田村素称“灯彩之乡”，田村花灯源于唐代，盛于宋朝，迄今已有1300多年历史了，某公司生产了一种田村花灯，每件田村花灯制造成本为20元．设销售单价x（元），每日销售量y（件）、每日的利润w（元）．在试销过程中，每日销售量y（件）、每日的利润w（元）与销售单价x（元）之间存在一定的关系，其几组对应量如下表所示：

销售单价x（元）

30

31

32

40

销售量y（件）

40

38

36

20

(1)、根据表中数据的规律、分別写出每日销售量y（件）、每日利润w（元）关于销售单价x（元）之间的函数表达式（利润＝（销售单价﹣成本单价）×销售件数）．

(2)、当销售单价为多少元时，公司每日能够获得最大利润？最大利润是多少？

查看试题解析
21. 如图，AB是⊙O的直径，点C是⊙O上一点，连接AC、BC ，过点C作∠BCP＝∠BAC ，交AB的延长线于点P ，弦CD平分∠ACB ，交AB于点E ，连接OC、AD、BD ．

(1)、求证：PC为⊙O的切线；

(2)、若OC＝5，OE＝1，求PC的长．

查看试题解析
22. 今年以来，因生猪受到猪瘟的影响，导致多地猪肉价格连续上涨，引起了民众与政府的高度关注，当市场猪肉的平均价格每千克达到一定的单价时，政府将投入储备猪肉以平抑猪肉价格．据统计：从今年年初至9月20日，猪肉价格不断上涨，9月20日比年初价格上涨了60%、某市民于某超市今年9月20日购买3千克猪肉花120元钱．

(1)、问：那么今年年初猪肉的价格为每千克多少元？

(2)、现在某超市以每千克30元的猪肉进货，按9月20日价格出售，平均一天能销售出100千克，经调查表明：猪肉的售价每千克下降1元，其日销售量就增加20千克，超市为了实现销售猪肉每天有1120元的销售利润，为了尽可能让顾客优惠应该每千克定价为多少元？

查看试题解析
23. 如图1，在锐角△ABC中，AB＝5，AC＝4 $\sqrt{2}$ ，∠ACB＝45°

(1)、计算：求BC的长；

(2)、操作：将图1中的△ABC绕点B按逆时针方向旋转，得到△A₁BC₁ ．如图2，当点C₁在线段CA的延长线上时．
①求∠CC₁A₁的度数；

②求四边形A₁BCC₁的面积；

(3)、探究：如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转所得到的△A₁BC₁中，点P的对应点是点P₁ ，求线段EP₁长度的最大值与最小值．

查看试题解析
24. 已知：抛物线C₁：y＝﹣（x+m）²+m²（m＞0），抛物线C₂：y＝（x﹣n）²+n²（n＞0），称抛物线C₁ ， C₂互为派对抛物线，例如抛物线C₁：y＝﹣（x+1）²+1与抛物线C₂：y＝（x﹣ $\sqrt{2}$ ）²+2是派对抛物线，已知派对抛物线C₁ ， C₂的顶点分别为A，B，抛物线C₁的对称轴交抛物线C₂于C，抛物线C₂的对称轴交抛物线C₁与D．

(1)、已知抛物线①y＝﹣x²﹣2x，②y＝（x﹣3）²+3，③y＝（x﹣ $\sqrt{2}$ ）²+2，④y＝x²﹣x+ $\frac{1}{2}$ ，则抛物线①②③④中互为派对抛物线的是（请在横线上填写抛物线的数字序号）；

(2)、如图1，当m＝1，n＝2时，证明AC＝BD；

(3)、如图2，连接AB，CD交于点F，延长BA交x轴的负半轴于点E，记BD交x轴于G，CD交x轴于点H，∠BEO＝∠BDC．
①求证：四边形ACBD是菱形；

②若已知抛物线C₂：y＝（x﹣2）²+4，请求出m的值．

查看试题解析

销售单价x（元）	30	31	32	40
销售量y（件）	40	38	36	20