江西省赣州市信丰县2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程x（x﹣5）＝0的解是（）.

A、0 B、5 C、0和5 D、0和﹣5

查看试题解析
2. 近几年我国国产汽车行业蓬勃发展，下列汽车标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 用配方法解一元二次方程 $x^{2} - 4 x + 1 = 0$ 时，下列变形正确的是（）．

A、 ${(x - 2)}^{2} = 1$ B、 ${(x - 2)}^{2} = 5$ C、 ${(x + 2)}^{2} = 3$ D、 ${(x - 2)}^{2} = 3$

查看试题解析
4. 关于x的一元二次方程kx²+2x+1＝0有两个不相等的实数根，则k的取值范围是（）

A、k＞﹣1 B、k≥﹣1 C、k≠0 D、k＜1且k≠0

查看试题解析
5. 如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为E，连接CO，AD，∠BAD=20°，则下列说法中正确的是（）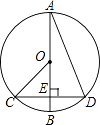

A、AD=2OB B、CE=EO C、∠OCE=40° D、∠BOC=2∠BAD

查看试题解析
6. 关于抛物线y＝x²－（a＋1）x＋a－2，下列说法错误的是（）

A、开口向上 B、当a＝2时，经过坐标原点O C、a＞0时，对称轴在y轴左侧 D、不论a为何值，都经过定点（1，－2）

查看试题解析

二、填空题

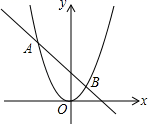
7. 在平面直角坐标系中，点（﹣2，3）关于原点对称的点的坐标是．

查看试题解析
8. 如图，抛物线y＝ax²与直线y＝bx+c的两个交点坐标分别为A(﹣2，4)，B(1，1)，则不等式ax²＜bx+c的解集是.

查看试题解析
9. 《九章算术》中记载有一问题“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”小辉同学根据原文题意，画出圆材截面图如图所示，已知：锯口深1寸，锯道 $A B = 1$ 尺（1尺=10寸），则该圆材的直径为寸.

查看试题解析
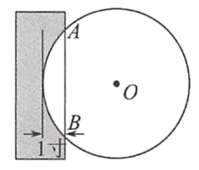10. 一元二次方程 $x^{2} - 4 x + 2 = 0$ 的两根为 $x_{1}$ , $x_{2}$ ,则 $x_{1}^{2} - 4 x_{1} + 2 x_{1} x_{2}$ 的值为 .

查看试题解析
11. 如图，在矩形ABCD中，AD=3，将矩形ABCD绕点A逆时针旋转，得到矩形AEFG，点B的对应点E落在CD上，且DE=EF，则AB的长为．

查看试题解析
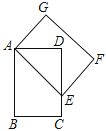12. 已知抛物线y=x²+2x﹣3与x轴交于A，B两点（点A在点B的左侧），将这条抛物线向右平移m（m＞0）个单位长度，平移后的抛物线与x轴交于C，D两点（点C在点D的左侧），若B，C是线段AD的三等分点，则m的值为.

查看试题解析

三、解答题

13. 解方程：x²﹣2x﹣3=0；

查看试题解析
14. 如图，在△ABC中，已知∠ABC＝30°，将△ABC绕点B逆时针旋转50后得到△A′BC′．已知A′C′∥BC ，求∠A的度数．

查看试题解析

15. 已知二次函数

y = a x^{2} + b x + c

图象上部分点的横坐标

x

、纵坐标

y

的对应值如下表：

$x$	…	0	1	2	3	4	…
$y$	…	-3	-4	-3	0	5	…

(1)、求该二次函数的表达式；

(2)、直接写出该二次函数图象与

x

轴的交点坐标.

查看试题解析

16. 如图，⊙O是△ABC的外接圆，AB＝AC ， P是⊙O上一点，请你只用无刻度的直尺，分别画出图①和图②中∠P的平分线．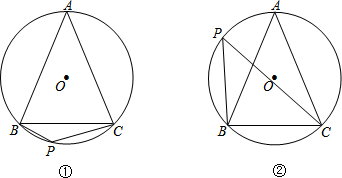

查看试题解析
17. 改善小区环境，争创文明家园.如图所示，某社区决定在一块长（ $A D$ ）16 $m$ ，宽（ $A B$ ）9 $m$ 的矩形场地 $A B C D$ 上修建三条同样宽的小路，其中两条与 $A B$ 平行，另一条与 $A D$ 平行，其余部分种草.要使草坪部分的总面积为112 $m^{2}$ ，则小路的宽应为多少？

查看试题解析
18. 如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．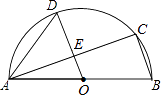

(1)、若∠B=70°，求∠CAD的度数；

(2)、若AB=4，AC=3，求DE的长．

查看试题解析
19. 如图，Rt△ABC中，∠C＝90°，将△ABC沿AB向下翻折后，再绕点A按顺时针方向旋转α度（α＜∠BAC），得到Rt△ADE ，其中斜边AE交BC于点F ，直角边DE分别交AB ， BC于点G ， H ．

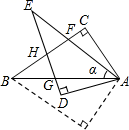(1)、判断∠CAF与∠DAG是否相等，并说明理由．

(2)、求证：△ACF≌△ADG ．

查看试题解析
20. 如图：已知抛物线y＝ax²＋bx(a≠0)经过A（3，0），B（4，4）两点.

(1)、求抛物线解析式.

(2)、将直线OB向下平移m个单位后，得到的直线与抛物线只有一个公共点D，求m值及交点D的坐标.

查看试题解析
21. 某厂家生产一种新型电子产品，制造时每件的成本为40元，通过试销发现，销售量 $y ($ 万件 $)$ 与销售单价 $x ($ 元 $)$ 之间符合一次函数关系，其图象如图所示.

(1)、求y与x的函数关系式；

(2)、物价部门规定：这种电子产品销售单价不得超过每件80元，那么，当销售单价x定为每件多少元时，厂家每月获得的利润 $(w)$ 最大？最大利润是多少？

查看试题解析
22. 已知：如图，△ABC内接于⊙O，AB为直径，∠CBA的平分线交AC于点F，交⊙O于点D，DE⊥AB于点E，且交AC于点P，连结AD．

(1)、求证：∠DAC=∠DBA；

(2)、求证：PD=PF；

(3)、连接CD，若CD﹦3，BD﹦4，求⊙O的半径和DE的长．

查看试题解析
23. 如图，已知二次函数y=ax²+bx+c的图象与x轴相交于A（﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）．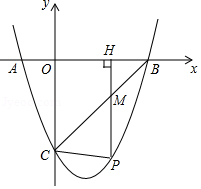

(1)、求这个二次函数的表达式；

(2)、若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与BC交于点M，连接PC．
①求线段PM的最大值；
②当△PCM是以PM为一腰的等腰三角形时，求点P的坐标．

查看试题解析
24. 问题背景：如图①，在四边形ADBC中，∠ACB＝∠ADB＝90°，AD＝BD，探究线段AC、BC、CD之间的数量关系.
小吴同学探究此问题的思路是：将ΔBCD绕点D逆时针旋转90°到ΔAED处，点B、C分别落在点A、E处（如图②），易证点C、A、E在同一条直线上，并且ΔCDE是等腰直角三角形，所以CE＝ $\sqrt{2}$ CD，从而得出结论：AC+BC＝ $\sqrt{2}$ CD．

图①

图②

图③

图④

简单应用：

(1)、在图①中，若AC＝ $\sqrt{2}$ ，BC＝2 $\sqrt{2}$ ，则CD＝.

(2)、如图③，AB是⊙O的直径，点C、D在⊙O上，弧AD＝弧BD，若AB＝13，BC＝12，求CD的长.

(3)、拓展延伸：
如图④，∠ACB＝∠ADB＝90°，AD＝BD，若AC＝m，BC＝n（m<n），求CD的长（用含m，n的代数式表示）.

查看试题解析