江西省赣州市宁都县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 下列手机手势解锁图案中,是中心对称图形的是( )A、
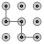 B、
B、 C、
C、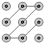 D、
D、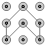 2. 用配方法解方程x2﹣x﹣1=0时,应将其变形为( )A、(x﹣)2= B、(x+)2= C、(x﹣)2=0 D、(x﹣)2=3. 如果将抛物线 向下平移1个单位,那么所得新抛物线的表达式是( )
2. 用配方法解方程x2﹣x﹣1=0时,应将其变形为( )A、(x﹣)2= B、(x+)2= C、(x﹣)2=0 D、(x﹣)2=3. 如果将抛物线 向下平移1个单位,那么所得新抛物线的表达式是( )
A、 B、 C、 D、4. 已知二次函数 的图象与x轴的一个交点为 ,则关于x的方程 的两实数根分别是A、1和 B、1和 C、1和2 D、1和35. 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内 上的一点,若 ,则 的度数是 A、45° B、60° C、65° D、70°6. 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( )
A、45° B、60° C、65° D、70°6. 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( ) A、-3 B、1 C、5 D、8
A、-3 B、1 C、5 D、8二、填空题
-
7. 已知 是二次函数,则 .8. 已知m是关于x的方程 的一个根,则 = .9. 菱形的两条对角线长分别是方程 的两实根,则菱形的面积为 .10. 宁都县某脐橙园2016年产量为1000吨,2018年产量为1440吨,求该脐橙园脐橙产量的年平均增长率,设该脐橙园脐橙产量的年平均增长量为x,则根据题意可列方程为 .11. 已知抛物线y=a(x+1)2+k(a>0)经过点(﹣4,y1),(1,y2),则y1y2(填“>”,“=”,或“<”).12. 等腰三角形三边长分别为 ,且 是关于 的一元二次方程 的两根,则 的值为13. 如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1=.
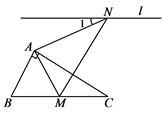 14. 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千。拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为米。
14. 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千。拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为米。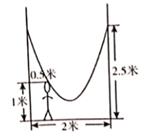
三、解答题
-
15.(1)、计算﹣22+8÷(﹣2)3﹣2×( )(2)、解方程:3x(x﹣2)=2(x﹣2)16. 已知关于x的方程 ,求证:不论k取任何实数,该方程都有实数根.17. 校运会期间,小捷同学积极参与各项活动.在铅球项目中,他掷出的铅球在场地上压出一个小坑(图示是其主视图),经测量,其中坑宽AB为8cm , 小坑的最大深度为2cm , 请帮助小捷同学计算铅球的半径OA的长为多少?
 18.
18.⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
 (1)、如图1,AC=BC(2)、如图2,直线l与⊙O相切于点P,且l∥BC。
(1)、如图1,AC=BC(2)、如图2,直线l与⊙O相切于点P,且l∥BC。
19. 如图,AB是⊙O的直径,弦CD⊥AB于点E , 点G在直径DF的延长线上,∠D=∠G=30°. (1)、求证:CG是⊙O的切线(2)、若CD=6,求GF的长20. 如图,△ABC是⊙O的内接三角形,点C是优弧AB上一个动点(不与A、B重合).设∠OAB=α,∠C=β
(1)、求证:CG是⊙O的切线(2)、若CD=6,求GF的长20. 如图,△ABC是⊙O的内接三角形,点C是优弧AB上一个动点(不与A、B重合).设∠OAB=α,∠C=β (1)、当α=35°时,求β的度数;(2)、猜想α与β之间的关系,并给予证明.21. 如图,⊙M与x轴交于A、B两点,与y轴切于点C,且OA,OB的长是方程x2﹣4x+3=0的解.
(1)、当α=35°时,求β的度数;(2)、猜想α与β之间的关系,并给予证明.21. 如图,⊙M与x轴交于A、B两点,与y轴切于点C,且OA,OB的长是方程x2﹣4x+3=0的解. (1)、求M点的坐标.(2)、若P是⊙M上一个动点(不包括A、B两点),求∠APB的度数.22. 某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)、求M点的坐标.(2)、若P是⊙M上一个动点(不包括A、B两点),求∠APB的度数.22. 某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)、求出y与x的函数关系式;
(2)、当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?(3)、设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
23. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b. (1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.
(1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.