广西河池市大化瑶族自治县2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-09-27 类型:期末考试
一、单选题
-
1. 下列四幅图案中,能通过平移图得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在实数π , , , 中,是无理数的是( )A、p B、 C、 D、3. 不等式组 的解集在数轴上表示为( )A、
2. 在实数π , , , 中,是无理数的是( )A、p B、 C、 D、3. 不等式组 的解集在数轴上表示为( )A、 B、
B、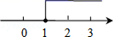 C、
C、 D、
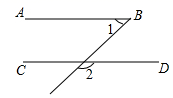
D、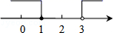 4. 下列调查方式合适的是( )A、疫情期间,为了解进校人员体温情况采用抽样调查的方式 B、了解炮弹的杀伤力,采用全面调查的方式 C、对中央台“新闻联播”收视率的调查,采用全面调查的方式 D、对哒件小镇食品合格情况的调查,采用抽样调查的方式5. 若点P 在 轴上,则点P的坐标为( )A、(0,-2) B、(4,0) C、(2,0) D、(0,-4)6. 若 是关于 的二元一次方程 的解,则 的值为( )A、 B、 C、 D、7. 如图,已知∠1=∠2,∠3=30°,则∠B的度数是( )
4. 下列调查方式合适的是( )A、疫情期间,为了解进校人员体温情况采用抽样调查的方式 B、了解炮弹的杀伤力,采用全面调查的方式 C、对中央台“新闻联播”收视率的调查,采用全面调查的方式 D、对哒件小镇食品合格情况的调查,采用抽样调查的方式5. 若点P 在 轴上,则点P的坐标为( )A、(0,-2) B、(4,0) C、(2,0) D、(0,-4)6. 若 是关于 的二元一次方程 的解,则 的值为( )A、 B、 C、 D、7. 如图,已知∠1=∠2,∠3=30°,则∠B的度数是( )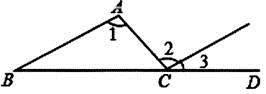 A、 B、 C、 D、8. 一个正数的两个平方根分别是2a−1与−a+2,则a的值为( )A、-1 B、1 C、-2 D、29. 下列说法正确的个数有( )
A、 B、 C、 D、8. 一个正数的两个平方根分别是2a−1与−a+2,则a的值为( )A、-1 B、1 C、-2 D、29. 下列说法正确的个数有( )①同位角相等②过一点有且只有一条直线与已知直线垂直③过一点有且只有一条直线与已知直线平行④若a∥b,b∥c,则a∥c.
A、1个 B、2个 C、3个 D、4个10. 如图, 的度数比 的度数的两倍少 ,设 和 的度数分别为 ,那么下面可以求出这两个角的度数的方程组是( )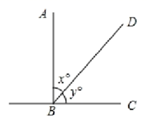 A、 B、 C、 D、11. 若关于x的一元一次不等式组 的解集是x<5,则m的取值范围是( )A、m≥5 B、m>5 C、m≤5 D、m<512. 计算 的结果为( )A、 B、 C、 D、
A、 B、 C、 D、11. 若关于x的一元一次不等式组 的解集是x<5,则m的取值范围是( )A、m≥5 B、m>5 C、m≤5 D、m<512. 计算 的结果为( )A、 B、 C、 D、二、填空题
-
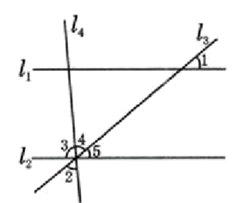
13. 9的平方根是 ,使分式有意义的x的取值范围是 .14. 把“不相等的角不是对顶角”改写成“如果…那么…”的形式是.15. 如图,已知 ,则 的度数是.
 16. 在一个扇形统计图中,有一个扇形占所在圆的40%,则这个扇形圆心角是.17. 平面直角坐标系中有一点 ,点 到 轴距离为 ,点 的纵坐标为 ,则点 的坐标是18. 已知关于 的不等式组 只有 个整数解,则实数 的取值范围是
16. 在一个扇形统计图中,有一个扇形占所在圆的40%,则这个扇形圆心角是.17. 平面直角坐标系中有一点 ,点 到 轴距离为 ,点 的纵坐标为 ,则点 的坐标是18. 已知关于 的不等式组 只有 个整数解,则实数 的取值范围是三、解答题
-
19. 计算:(1)、(2)、20.(1)、解不等式(2)、解方程组21. 如图, ,那么直线 与 平行吗?为什么?
 22. 如图所示, 在方格中,方格纸中的每个小方格都是边长为 个单位的正方形,三个顶点的坐标分别是 ,先将 向上平移 个单位长度,再向右平移 个单位长度,得到 ,已知点 的对应点分别是点
22. 如图所示, 在方格中,方格纸中的每个小方格都是边长为 个单位的正方形,三个顶点的坐标分别是 ,先将 向上平移 个单位长度,再向右平移 个单位长度,得到 ,已知点 的对应点分别是点 (1)、在图中画出(2)、写出点 的坐标(3)、求出 的面积23. 为打造平安校园,增强学生安全防范意识,某校组织了全校 名学生参加校园安全网络知识竞赛,赛后随机抽取了其中 名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
(1)、在图中画出(2)、写出点 的坐标(3)、求出 的面积23. 为打造平安校园,增强学生安全防范意识,某校组织了全校 名学生参加校园安全网络知识竞赛,赛后随机抽取了其中 名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.成绩 /分
频数
百分比
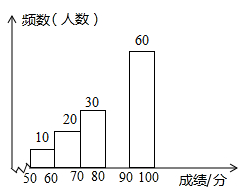
请根据图、表提供的信息,解答下列各题:
(1)、表中 , , 请补全频数分布直方图;(2)、若用扇形统计图来描述成绩分布情况,则 对应扇形的圆心角的度数是 ;(3)、若成绩在 分以上(包括 分)为合格,则参加这次竞赛的 名学生中成绩合格的大约有多少名?24. 若方程组 与方程组 的解相同,求 的值25. 为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛.为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同).已知购买 个足球和 个篮球共需 元;足球单价比篮球单价的 倍少 元.(1)、足球和篮球的单价各是多少元?.(2)、根据学校实际情况,需一次性购买足球和篮球共 个,但要求购买足球和篮球的总费用不超过 元,学校最多可以购买多少个足球?26. 已知AB∥CD,在AB,CD内有一条折线EGF.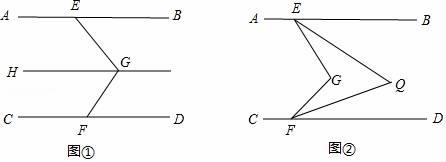 (1)、如图①,过点G作GH∥AB,求证:∠BEG+∠DFG=∠EGF;(2)、如图②,已知∠BEG的平分线与∠DFG的平分线相交于点Q,请探究∠EGF与∠EQF的数量关系,并说明理由.
(1)、如图①,过点G作GH∥AB,求证:∠BEG+∠DFG=∠EGF;(2)、如图②,已知∠BEG的平分线与∠DFG的平分线相交于点Q,请探究∠EGF与∠EQF的数量关系,并说明理由.