江西省赣州市会昌县2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 把抛物线 $y = - \frac{1}{2} x^{2}$ 先向左平移1个单位，再向下平移2个单位长度后，所得的函数表达式为（）

A、 $y = - \frac{1}{2} {(x + 1)}^{2} + 2$ B、 $y = - \frac{1}{2} {(x + 1)}^{2} - 2$ C、 $y = - \frac{1}{2} {(x - 1)}^{2} + 2$ D、 $y = - \frac{1}{2} {(x - 1)}^{2} - 2$

查看试题解析
3. 用配方法解一元二次方程x²﹣6x+8=0时，则方程变形正确的是（）

A、（x﹣3）²=17 B、（x+3）²=17 C、（x﹣3）²=1 D、（x+3）²=1

查看试题解析
4. 中国“一带一路”战略给沿线国家和地区带来很大的经济效益，沿线某地区居民2015年年收入200美元，预计2017年年收入将达到1000美元，设2015年到2017年该地区居民年人均收入平均增长率为x，可列方程为（）

A、200（1+2x）＝1000 B、200+2x＝1000 C、200（1+x²）＝1000 D、200（1+x）²＝1000

查看试题解析
5. 已知二次函数y=ax²+4ax+c的图象与x轴的一个交点为（﹣1，0），则它与x轴的另一个交点的坐标是（）

A、（﹣3，0） B、（3，0） C、（1，0） D、（﹣2，0）

查看试题解析
6. 已知二次函数y=ax²+bx+c的图象如图所示，对称轴为x=1，经过点（-1，0），有下列结论：①abc＜0；②a+c＞b；③3a+c=0；④a+b＞m（am+b）（其中m≠1）其中正确的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 二次函数y=﹣x²﹣2x+3的顶点坐标为．

查看试题解析
8. 在平面直角坐标系中，将点P（﹣3，2）绕点O（0，0）顺时针旋转90°，所得到的对应点P′的坐标为．

查看试题解析
9. 若A（﹣4，y₁）、B（﹣3，y₂）、C（1，y₃）为二次函数y＝（x+2）²+1的图象上的三点，则y₁、y₂、y₃的大小关系用“＞”连接起来是．

查看试题解析
10.
如图，一块矩形铁皮的长是宽的2倍，将这个铁皮的四角各剪去一个边长为3cm的小正方形，做成一个无盖的盒子，若盒子的容积是240cm³ ，则原铁皮的宽为　 cm．

查看试题解析
11. 如图，△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形，点C恰好在边AB上．若∠AOD=100°，则∠D的度数是°．

查看试题解析

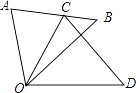
三、解答题

12. 如图，

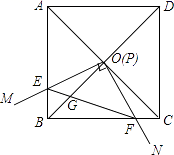
边长为1的正方形ABCD的对角线AC、BD相交于点O，有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是．

⑴EF= $\sqrt{2}$ OE；⑵S_四边形_OEBF：S_正方形_ABCD=1：4；⑶BE+BF= $\sqrt{2}$ OA；⑷在旋转过程中，当△BEF与△COF的面积之和最大时，AE= $\frac{3}{4}$ ．

查看试题解析
13. 解下列方程

(1)、x²﹣6x＝0

(2)、2x²﹣5x+2＝0

查看试题解析
14. 在平面直角坐标系中，二次函数y＝ax²+bx+3的图象经过点A（3，0）和点B（4，3）．

(1)、求二次函数的表达式；

(2)、求二次函数图象的顶点坐标和对称轴．

(3)、直接画出函数的图象（不列表）．

查看试题解析
15. 如图，已知在△ABC中，∠A＝60°，∠C＝90°，将△ABC绕点B顺时针旋转150°，得到△DBE ．请仅用无刻度的直尺，按要求画图（保留画图痕迹，在图中标出字母，并在图下方表示出所画图形）．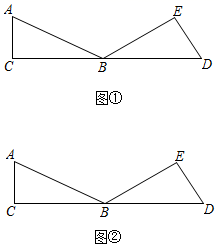

(1)、在图①中，画一个等边三角形；

(2)、在图②中，画一个等腰直角三角形．

查看试题解析
16. 如图1，在平行四边形ABCD中，对角线BD⊥AB ，以BD为对称轴将△ABD翻折，点A的对应点为A′，连接A′C ，得到图2．
推理证明

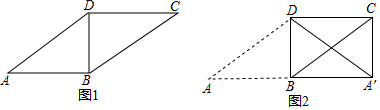(1)、求证：四边形A′BDC是矩形；

(2)、在图1中将△ABD或△BDC进行平移、旋转或轴对称变换，重新构造一个特殊四边形．
要求：①画出图形，标明字母；②写出构图过程及构造的特殊四边形的名称．（不要求证明）

查看试题解析
17. 关于x的方程x²﹣2（k﹣1）x+k²＝0有两个实数根x₁、x₂ ．

(1)、求k的取值范围；

(2)、若x₁+x₂＝1﹣x₁x₂ ，求k的值．

查看试题解析
18. 在平面直角坐标系xOy中，△ABC的位置如图所示.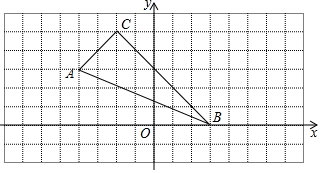

(1)、分别写出△ABC各个顶点的坐标；

(2)、分别写出顶点A关于x轴对称的点A′的坐标、顶点B关于y轴对称的点B′的坐标及顶点C关于原点对称的点C′的坐标；

(3)、求线段BC的长.

查看试题解析
19. 二次函数y＝ax²＋bx＋c的图象如图所示，根据图象解答下列问题：

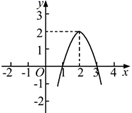(1)、写出方程ax²＋bx＋c＝0的两个根；

(2)、当x为何值时，y＞0？当x为何值时，y＜0?

(3)、写出y随x的增大而减小的自变量x的取值范围．

查看试题解析
20. 如图，在△ABC中，∠B＝90°，AB＝6cm ， BC＝8cm ，点P从A点出发沿AB边向B以1cm/s的速度移动，点Q从B点出发沿BC向C点以2cm/s的速度移动，当其中一个点到达终点时两个点同时停止运动，在两个点运动过程中，请回答：

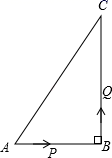(1)、经过多少时间，△PBQ的面积是5cm²？

(2)、请你利用配方法，求出经过多少时间，四边形APQC面积最小？并求出这个最小值．

查看试题解析
21. 如图，已知△ABC中，AB=AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F.

(1)、求证： $Δ A E C ≅ Δ A D B$ ；

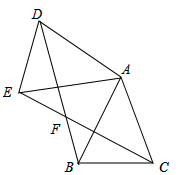(2)、若AB=2， $∠ B A C = 45^{°}$ ，当四边形ADFC是菱形时，求BF的长．

查看试题解析
22. 某商品的进价为每件20元，售价为每件30元，每个月可卖出180件；如果每件商品的售价每上涨1元，则每个月就会少卖出10件，但每件售价不能高于35元，设每件商品的售价上涨x元（x为整数），每个月的销售利润为y元．

(1)、求y与x的函数关系式，并直接写出自变量x的取值范围；求x为何值时y的值为1920；

(2)、每件商品的售价为多少元时，每个月可获得最大利润？最大利润是多少．

查看试题解析
23. 如图，抛物线经过点A(4，0)、B(﹣2，0)、C(0，﹣4)

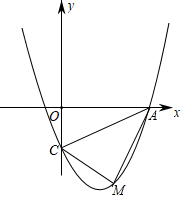(1)、求抛物线的解析式；

(2)、在抛物线AC段上是否存在点M，使△ACM的面积为3，求出在此时M的坐标，若不存在，说明理由.

查看试题解析