江西省抚州市南丰县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20cm,则它的宽约为( )A、12.36 cm B、13.6 cm C、32.36 cm D、7.64 cm2. 一元二次方程 配方后可化为( )A、 B、 C、 D、3. 如图所示,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为16,则OH的长等于( )
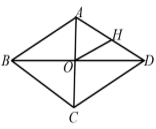 A、2 B、3 C、4 D、64. 不同颜色的丝带,代表着不同的意义--象征“平安归来”的黄丝带,象征“健康归来”的绿丝带,如图所示,丝带重叠部分形成的图形是( )
A、2 B、3 C、4 D、64. 不同颜色的丝带,代表着不同的意义--象征“平安归来”的黄丝带,象征“健康归来”的绿丝带,如图所示,丝带重叠部分形成的图形是( ) A、矩形 B、正方形 C、菱形 D、等腰梯形5. 在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任可其他区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的频率是0.2,则估计盒子中大约有红球( )
A、矩形 B、正方形 C、菱形 D、等腰梯形5. 在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任可其他区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的频率是0.2,则估计盒子中大约有红球( )
A、16个 B、20个 C、25个 D、30个6. 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 若关于 的方程 有整数根,则 的值可以是(只填一个).8. 某药品原价是100元,经连续两次降价后,价格变为64元,如果每次降价的百分率是一样的,那么每次降价的百分率是;9. 如图,E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE= .
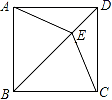 10. 如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于 .
10. 如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于 .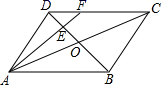 11. 如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为.
11. 如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为.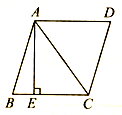 12. 如图,矩形ABCD对角线AC、BD交于点O,边AB=6,AD=8,四边形OCED为菱形,若将菱形OCED绕点O旋转一周,旋转过程中OE与矩形ABCD的边的交点始终为M,则线段ME的长度可取的整数值为 .
12. 如图,矩形ABCD对角线AC、BD交于点O,边AB=6,AD=8,四边形OCED为菱形,若将菱形OCED绕点O旋转一周,旋转过程中OE与矩形ABCD的边的交点始终为M,则线段ME的长度可取的整数值为 .
三、解答题
-
13.(1)、解方程:(2)、一个两位数字,十位数字比个位数字大3,而这两个数字之积等于这个两位数的 ,求这个两位数.14. 如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.求证:四边形EGFH是菱形.
 15. 甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选出2名同学打第一场比赛.(1)、已确定甲打第一场,再从其余3名同学中随机选取1名,求恰好选中乙同学的概率.(2)、随机选取2名同学,求其中有乙同学的概率(用表格或树状图分析).16. 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x , y轴的正半轴上.点Q在对角线OB上,且QO=OC , 连接CQ并延长CQ交边AB于点P . 求点P的坐标.
15. 甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选出2名同学打第一场比赛.(1)、已确定甲打第一场,再从其余3名同学中随机选取1名,求恰好选中乙同学的概率.(2)、随机选取2名同学,求其中有乙同学的概率(用表格或树状图分析).16. 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x , y轴的正半轴上.点Q在对角线OB上,且QO=OC , 连接CQ并延长CQ交边AB于点P . 求点P的坐标. 17. 仅用无刻度的直尺完成下列画图.
17. 仅用无刻度的直尺完成下列画图. (1)、如图1,M是正方形ABCD内一定点,请过M画出一条直线l1将正方形ABCD的面积两等分.(2)、如图2,M是网格正方形ABCD内一固定格点,请画出两条直线l2 , l3(要求其中一条直线必须过点M)将正方形ABCD的面积四等分.18. 已知 , 是关于 的一元二次方程 的两个实数根.(1)、求a的取值范围.(2)、若 ,求 的值.19. 某商场销售一批名牌衬衫,平均每天可以销售20件,每件盈利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天多售出2件,若商场平均每天要盈利1200元,每件衬衫应降价多少元?20. 如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)、如图1,M是正方形ABCD内一定点,请过M画出一条直线l1将正方形ABCD的面积两等分.(2)、如图2,M是网格正方形ABCD内一固定格点,请画出两条直线l2 , l3(要求其中一条直线必须过点M)将正方形ABCD的面积四等分.18. 已知 , 是关于 的一元二次方程 的两个实数根.(1)、求a的取值范围.(2)、若 ,求 的值.19. 某商场销售一批名牌衬衫,平均每天可以销售20件,每件盈利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天多售出2件,若商场平均每天要盈利1200元,每件衬衫应降价多少元?20. 如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE. (1)、求证:四边形ABCD是矩形;(2)、若AB=4,求△OEC的面积.21. 如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DC=4DF,连接EF并延长交BC的延长线于点G.
(1)、求证:四边形ABCD是矩形;(2)、若AB=4,求△OEC的面积.21. 如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DC=4DF,连接EF并延长交BC的延长线于点G. (1)、求证:△ABE∽△DEF;(2)、若正方形的边长为16,求BG的长.22. 如图,在边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿边BC向点C运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动设点F的运动时间为t秒.
(1)、求证:△ABE∽△DEF;(2)、若正方形的边长为16,求BG的长.22. 如图,在边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿边BC向点C运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动设点F的运动时间为t秒.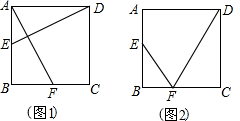 (1)、如图1,连接DE,AF.若DE⊥AF,求t的值;(2)、如图2,连结EF,DF.当t为何值时,△EBF∽△DCF?23. 在四边形 中,对角线 、 相交于点 ,将 绕点 按逆时针方向旋转得到 ,旋转角为θ(0°<θ<90°),连接 、 , 与 交于点 .
(1)、如图1,连接DE,AF.若DE⊥AF,求t的值;(2)、如图2,连结EF,DF.当t为何值时,△EBF∽△DCF?23. 在四边形 中,对角线 、 相交于点 ,将 绕点 按逆时针方向旋转得到 ,旋转角为θ(0°<θ<90°),连接 、 , 与 交于点 . (1)、如图1,若四边形 是正方形.
(1)、如图1,若四边形 是正方形.①求证: ≌ .
②请直接写出 与 的位置关系.
(2)、如图2,若四边形 是菱形, , ,设 .判断 与 的位置关系,说明理由,并求出 的值.(3)、如图3,若四边形 是平行四边形, , ,连接 ,设 .请直接写出 的值和 的值.