贵州省毕节市赫章县2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-09-27 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中，既是轴对称图形又是中心对称图形的是 $($ 　　 $)$

A、 B、 C、 D、

查看试题解析
2. 某种冠状病毒的直径120纳米，1纳米 $= 10^{- 9}$ 米，则这种冠状病毒的直径（单位是米）用科学记数法表示为（）

A、 $120 \times 10^{- 9}$ 米 B、 $1.2 \times 10^{- 8}$ 米 C、 $1.2 \times 10^{- 7}$ 米 D、 $1.2 \times 10^{- 6}$ 米

查看试题解析
3. 下列由左到右变形，属于因式分解的是（）

A、 $(2 x + 3) (2 x - 3) = 4 x^{2} - 9$ B、 $4 x^{2} + 18 x - 1 = 4 x (x + 2)$ C、 ${(a - b)}^{2} - 9 = (a - b + 3) (a - b - 3)$ D、 ${(x - 2 y)}^{2} = x^{2} - 4 x y + 4 y^{2}$

查看试题解析
4. 若 $\frac{a}{2} = \frac{b}{3}$ ，则 $\frac{a + b}{b}$ 的值为(　　)

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{5}{3}$ D、 $\frac{3}{5}$

查看试题解析
5. 在 $Δ A B C$ 中， $B C : A C : A B = 1 : 1 : \sqrt{2}$ ,则△ABC是（）

A、等腰三角形 B、钝角三角形 C、直角三角形 D、等腰直角三角形

查看试题解析
6. 通过平移图中的吉祥物“海宝”得到的图形是（）

A、 B、 C、 D、

查看试题解析
7. 已知a＋ $\frac{1}{a}$ ＝3，则a²＋ $\frac{1}{a^{2}}$ 等于（）

A、5 B、7 C、9 D、11

查看试题解析
8. 函数 $y = \frac{\sqrt{x - 2}}{x - 3}$ 的自变量x的取值范围是（　　）

A、x≥2 B、x≥3 C、x≠3 D、x≥2且x≠3

查看试题解析
9. 等腰三角形的两边长分别为4和9，则它的周长（　　）

A、17 B、22 C、17或22 D、21

查看试题解析
10. 如图，△ABC中，AB=AC，AB的垂直平分线交AB于D，交AC于E，且BE平分∠ABC，求∠A的度数为（）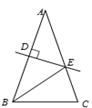

A、36° B、60° C、54 D、72°

查看试题解析
11. 贵州省将在2020年底前实现县城以上城区5G网络覆盖，5G网络峰值速率为4G网络峰值的10倍，在峰值速率下传输500兆数据，5G网络比4G网络快45秒，求这两种案例的峰值速率，设5G网络的峰值速率为每秒传输x兆数据，依题意列方程(　　　)

A、 $\frac{500}{x} - \frac{500}{10 x} = 45$ B、 $\frac{500}{x} - \frac{5000}{x} = 45$ C、 $\frac{500}{10 x} - \frac{500}{x} = 45$ D、 $\frac{5000}{x} - \frac{500}{x} = 45$

查看试题解析
12. 如图所示，直线l₁：y $= \frac{3}{2}$ x+6与直线l₂：y $= - \frac{5}{2}$ x﹣2交于点P（﹣2，3），不等式 $\frac{3}{2}$ x+6 $> - \frac{5}{2}$ x﹣2的解集是（）

A、x＞﹣2 B、x≥﹣2 C、x＜﹣2 D、x≤﹣2

查看试题解析
13. 已知三角形的三边a，b，c满足 $(b - a) (b {}^{2}+ c^{2}) = b a^{2} - a^{3}$ ，则△ABC是（）

A、等腰三角形 B、等腰直角三角形 C、等边三角形 D、等腰三角形或直角三角形

查看试题解析
14. 若不等式组 ${\begin{array}{l} x \geq a \\ x \leq b \end{array}$ 无解，则不等式组 ${\begin{array}{l} x > 3 - a \\ x < 3 - b \end{array}$ 的解集是（）

A、 $x > 3 - a$ B、 $x < 3 - b$ C、 $3 - a < x < 3 - b$ D、无解

查看试题解析
15. 如图，在△ABC中，∠C＝90°，以点B为圆心，以适当长为半径画弧交AB，BC于P、Q两点，再分别以点P，Q为圆心，大于 $\frac{1}{2}$ PQ的长为半径画弧，两弧相交于点N，射线BN交AC于点D.若AB＝10，AC＝8，则CD的长是（）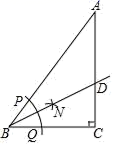

A、2 B、2.4 C、3 D、4

查看试题解析

二、填空题

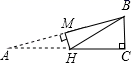
16. $16 x^{2} + k x y + 4 y^{2}$ 是一个完全平方式，则 $k =$

查看试题解析
17. 若x∶y∶z=2∶3∶4，则 $\frac{2 x + 3 y - z}{x - y + 2 z}$ 的值为.

查看试题解析
18. 若关于x，y的二元一次方程组 ${\begin{array}{l} 3 x - y = 1 + a \\ 2 y - x = 3 \end{array}$ 的解满足2x+y＜3，则a的取值范围是.

查看试题解析
19. 如图所示，在Rt△ABC中，∠C＝90°，∠A＝15°，将△ABC翻折，是顶点A与顶点B重合，折痕为MH，已知AH＝2，则BC等于.

查看试题解析
20. 将 $R t Δ A B C$ 沿 $B C$ 边向右平移得到 $R t Δ D E F ， A B = 8 ， B E = 6 ， D G = 3$ ，则阴影部分的面为.

查看试题解析

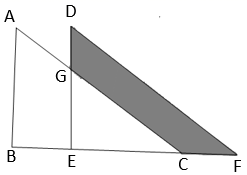
三、解答题

21. 已知 $a + b = 5, a b = 10$ ，求 $\frac{1}{2} a^{3} b + a^{2} b^{2} + \frac{1}{2} a b^{3}$ 的值.

查看试题解析
22. 解不等式组 ${\begin{array}{l} 5 x + 5 \geq 3 (x - 1) \\ \frac{1}{2} x - 1 < 4 - \frac{3}{2} x \end{array}$ (并把解集表示在数轴上，写出所有的整数解).

查看试题解析
23. 先化简 $\frac{x^{2} + 1}{x^{2} - 1} - \frac{x - 2}{x - 1} \div \frac{x^{2} - 4}{x^{2} + 2 x}$ ，再从 $- 3 \leq x \leq 3$ 中选一个合适的整数代入并求值.

查看试题解析
24. 如图，在平面直角坐标系中，三角形ABC的顶点坐标分别为 $A (- 2 ， 4)$ ， $B (- 5 ， - 1)$ ， $C (0 ， 1)$ ，把三角形ABC向右平移2个单位长度，再向下平移4个单位长度后得到三角形 $A^{'} B^{'} C^{'}$ .

(1)、画出三角形ABC和平移后 $A ’ B ’ C ’$ 的图形；

(2)、写出三个顶点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标；

(3)、求三角形ABC的面积.

查看试题解析
25. 新型冠状病毒肺炎疫情发生后，全社会积极参与疫情防控工作，某市为了尽快完成100万只口罩的生产任务，安排甲、乙两个大型工厂完成．已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍，并且在独立完成60万只口罩的生产任务时，甲厂比乙厂少用5天．问至少应安排两个工厂工作多少天才能完成任务？

查看试题解析

26. “绿水青山就是金山银山”，为保护生态环境，A，B两村准备各自清理所属区域养鱼网箱和捕鱼网箱，每村参加清理人数及总开支如下表：

村庄	清理养鱼网箱人数/人	清理捕鱼网箱人数/人	总支出/元
A	15	9	57000
B	10	16	68000

(1)、若两村清理同类渔具的人均支出费用一样，求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元；

(2)、在人均支出费用不变的情况下，为节约开支，两村准备抽调40人共同清理养鱼网箱和捕鱼网箱，要使总支出不超过102000元，且清理养鱼网箱人数小于清理捕鱼网箱人数，则有哪几种分配清理人员方案？

查看试题解析

27. 如图， $Δ A B C$ 为等边三角形， $A E = C D$ ， $A D$ 、 $B E$ 相交于点 $P$ ， $B Q ⊥ A D$ 于点 $Q$ ， $P Q = 3$ ， $P E = 1$ .

(1)、求证： $A D = B E$ ；

(2)、求 $A D$ 的长.

查看试题解析