重庆市万盛经济技术开发区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-27 类型:期末考试
一、选择题
-
1. 二次根式 中,x的取值范围是( )A、 B、 C、 D、2. 下列选择中,是直角三角形的三边长的是( )A、1,2,3 B、2,3,4 C、3,4,6 D、1, ,23. 已知函数y=x+k+1是正比例函数,则k的值为( )A、1 B、﹣1 C、0 D、±14. 下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差:
甲
乙
丙
丁
平均数(分)
92
95
95
92
方差
3.6
3.6
7.4
8.1
要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁5. 在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( )A、BC=CD B、AB=CD C、∠D=90° D、AD=BC6. 下列各式中,运算正确的是( )A、 =﹣2 B、 + = C、 × =4 D、2 ﹣ =27. 点A(x1 , y1)和B(x2 , y2)都在直线y=x﹣5上,且x1>x2 , 则y1与y2的关系是( )A、y1≥y2 B、y1=y2 C、y1<y2 D、y1>y28. 直角三角形中,两条直角边长分别是12和5,则斜边中线长是( )A、26 B、13 C、 D、6.59. 为了解某种电动汽车一次充电后行驶的里程数,抽检了10辆车,统计结果如图所示,则在一次充电后行驶的里程数这组数据中,众数和中位数分别是( ) A、220,220 B、220,210 C、200,220 D、230,21010. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
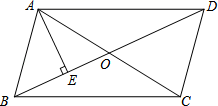
A、220,220 B、220,210 C、200,220 D、230,21010. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )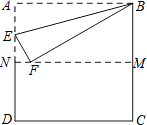 A、2 B、 C、 D、111. 小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
A、2 B、 C、 D、111. 小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:①小华先到达青少年宫;
②小华的速度是小明速度的2.5倍;
③a=24;④b=480.
其中正确的是( )
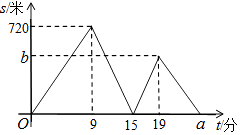 A、①②④ B、①②③ C、①③④ D、①②③④12. 若关于x的分式方程 =3+ 的解为整数,且一次函数y=(10﹣a)x+a的图象不经过第四象限,则符合题意的整数a的个数为( )A、1 B、2 C、3 D、4
A、①②④ B、①②③ C、①③④ D、①②③④12. 若关于x的分式方程 =3+ 的解为整数,且一次函数y=(10﹣a)x+a的图象不经过第四象限,则符合题意的整数a的个数为( )A、1 B、2 C、3 D、4二、填空题
-
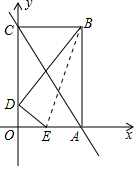
13. 在平行四边形ABCD中,∠A+∠C=200°,则∠A=.14. 把 化成最简二次根式的结果是.15. 根据图象,不等式kx>﹣x+3的解集是.
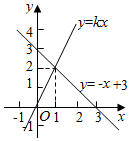 16. 在某次知识竞赛中,10名学生的成绩统计如表:
16. 在某次知识竞赛中,10名学生的成绩统计如表:得分(分)
60
70
80
90
100
人数(分)
1
1
5
2
1
则这10名学生成绩的平均数为.
17. 如图,所有阴影四边形都是正方形,两个空白三角形均为直角三角形,且A、B、C三个正方形的边长分别为2、3、4,则正方形D的面积为.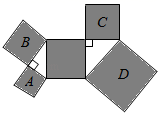 18. 如图,在边长为 的菱形 中, ,将 沿射线 的方向平移得到 ,分别连接 , , 则 的最小值为.
18. 如图,在边长为 的菱形 中, ,将 沿射线 的方向平移得到 ,分别连接 , , 则 的最小值为.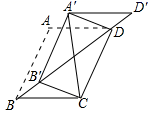
三、解答题
-
19.(1)、计算:( + )× ﹣ + ;(2)、已知直线y=kx+b经过(1,0),(2,3),求直线的解析式.20. 某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%、20%、30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如表(单位:分):
纸笔测试
实践能力
成长记录
甲
90
83
95
乙
96
82
94
丙
84
88
94
通过计算,确定学期总评成绩优秀的同学.
21. 如图,在▱ABCD中,点E,F在对角线AC上,且AE=CF.连接BE,BF,DE,DF. (1)、求证:△ABE≌△CDF;(2)、求证:四边形DEBF为平行四边形.22. 在6•26国际禁毒日到来之际,万盛经开区教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛,某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如表:
(1)、求证:△ABE≌△CDF;(2)、求证:四边形DEBF为平行四边形.22. 在6•26国际禁毒日到来之际,万盛经开区教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛,某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如表:初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
89
97
100
99
94
79
99
98
79
(整理、描述数据):按如表格分数段整理、描述这两组样本数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
a
b
12
初二人数
2
2
1
15
(分析数据):样本数据的平均数、中位数、满分数如表:
年级
平均数
中位数
满分数
初一
90.1
c
5
初二
92.8
97.5
4
(得出结论):
(1)、在上述统计表格中a= , b= , c=;(2)、哪个年级掌握禁毒知识的总体水平较好,试从两个方面说明理由;(3)、估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共有多少人?23. 如图①,矩形ABCD的四边上分别有E、F、G、H四点,顺次连接四点得到四边形EFGH.若∠1=∠2=∠3=∠4.则四边形EFGH为矩形ABCD的“反射四边形”. (1)、请在图②,图③中画出矩形ABCD的“反射四边形EFGH”.(2)、若AB=4,BC=8.请在图②,③任选其一,计算“反射四边形EFGH”的周长.24. 年初,武汉暴发新冠疫情,“一方有难,八方支援”,某地为助力武汉抗疫,紧急募集到一批物资运往武汉的A、B两县,用载重量为16吨的大货车8辆和载重量10吨的小货车10辆恰好一次性运完这批物资.运往A、B两县的运费标准如表:
(1)、请在图②,图③中画出矩形ABCD的“反射四边形EFGH”.(2)、若AB=4,BC=8.请在图②,③任选其一,计算“反射四边形EFGH”的周长.24. 年初,武汉暴发新冠疫情,“一方有难,八方支援”,某地为助力武汉抗疫,紧急募集到一批物资运往武汉的A、B两县,用载重量为16吨的大货车8辆和载重量10吨的小货车10辆恰好一次性运完这批物资.运往A、B两县的运费标准如表:运往地
车型
A县(元/辆)
B县(元/辆)
大货车
1080
1200
小货车
750
950
(1)、如果安排到A、B两县的货车都是9辆,设前往A县的大货车为x辆,前往A、B两县的总运费为y元,求出y与x的函数关系式(写出自变量的取值范围);(2)、在(1)的条件下,若运往A县的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.