辽宁省丹东市2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-09-27 类型：期末考试

进入出卷网下载

一、选择题

1. 下列是不等式的是（）

A、 $x + y$ B、 $3 x > 7$ C、 $2 x + 3 = 5$ D、 $x^{3} y^{2}$

查看试题解析
2. 下列图形中，是中心对称图形的是（）

A、等边三角形 B、正五边形 C、平行四边形 D、等腰直角三角形

查看试题解析
3. 下列各式中从左到右的变形中，是因式分解的是（）

A、 $m (a + b + c) = m a + m b + m c$ B、 $x^{2} + 6 x + 36 = {(x + 6)}^{2}$ C、 $a^{2} - b^{2} + 1 = (a + b) (a - b) + 1$ D、 $10 x^{2} - 5 x = 5 x (2 x - 1)$

查看试题解析
4. 若 $m < n$ ，则下列各式正确的是（）

A、 $- 3 m < - 3 n$ B、 $m + 1 < n + 1$ C、 $3 m > 3 n$ D、 $m - 1 > n - 1$

查看试题解析
5. 下列各式从左到右的变形一定正确的是（）

A、 $\frac{a + 3}{b + 3} = \frac{a}{b}$ B、 $\frac{a}{b} = \frac{a c}{b c}$ C、 $\frac{a}{b} = \frac{a^{3}}{b^{3}}$ D、 $\frac{a b}{3 a b} = \frac{1}{3}$

查看试题解析
6. 如图，在 $Δ A B C$ 中， $∠ C = 90^{°} ， D$ 是AC上一点， $D E ⊥ A B$ 于点E， $B E = B C$ 连接BD，若AC=8cm，则 $A D + D E$ 等于（）

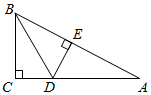A、6cm B、7cm C、8cm D、9cm

查看试题解析
7. 若关于x的分式方程 $\frac{x - 4}{x - 3} - 3 = \frac{a}{x - 3}$ 有增根，则a的值是（）

A、-1 B、-2 C、3 D、-3

查看试题解析
8. 如图，一次函数 $y_{1} = k x + 4$ 与 $y_{2} = x + m$ 的图象相交于点 $P (1 ， 3)$ ，则关于x的不等式 $k x + 4 < x + m$ 的解集是（）

A、 $x < 1$ B、 $x > 1$ C、 $x < 3$ D、 $x > 3$

查看试题解析
9. 如图， $▱ A B C D$ 的对角线AC，BD交于点O，AE平分 $∠ B A D$ ，交BC于点E，且 $∠ A D C = 60^{°} ， A B = \frac{1}{2} B C$ ，连接OE，下列结论① $∠ C A D = 30^{°}$ ；②OD=AB；③ $S_{▱ A B C D} = A C \cdot C D$ ；④ $S_{O E C D} = \frac{3}{2} S_{Δ A O D}$ ；其中成立的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

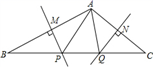
10. 如果分式 $\frac{x - 2}{x + 2}$ 有意义，那么x的取值范围是；

查看试题解析
11. 若一个多边形的内角和是900º，则这个多边形是边形.

查看试题解析
12. 若 $2 a - b = 4$ ，则 $4 a^{2} - 4 a b + b^{2} =$ .

查看试题解析
13. 如图，在△ABC中，若PM，QN分别垂直平分AB，AC，如果BC=10cm，则△APQ的周长为

查看试题解析
14. 如图，在 $Δ A B C$ 中， $A C = B C ， ∠ C = 90^{°} ， A D$ 是 $Δ A B C$ 的角平分线 $D E ⊥ A B$ ，垂足为E，若CD=6，则 $A C =$ .

查看试题解析
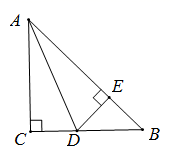15. 如图，平行四边形ABCD的对角线AC，BD交于点O，点E是AD的中点，△ $A E O$ 的周长为6，则△ $A B C$ 的周长为.

查看试题解析
16. 不等式 $6 + x \geq 4 x - 3$ 的非负整数解有个；

查看试题解析
17. 如图，平行四边形ABCD的对角线AC，BD交于点O，E，F是对角线AC上两点，给出下列4个条件：① $O E = O F$ ；②DE=BF；③ $∠ A D E = ∠ B C F$ ；④ $∠ A B E = ∠ C D F$ ，其中不能判定四边形DEBF是平行四边形的是；

查看试题解析
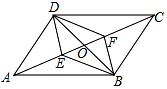18. 如图，在 $Δ A B C$ 中， $∠ C = 90^{°} ， A C = B C ， A B = 2 \sqrt{2} + 2$ ，点M，N分别是AB，AC上的动点，沿MN所在的直线折叠，使点A的对应点 $A^{'}$ 始终落在BC上， $Δ M A^{'} B$ 若为直角三角形，则BM的长为；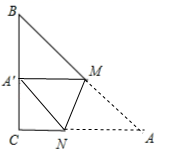

查看试题解析

三、解答题

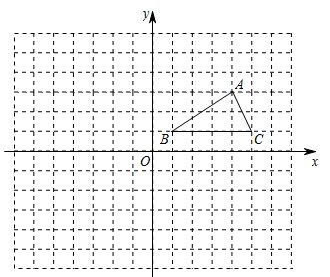
19. 计算：

(1)、因式分解 $5 a x^{2} - 5 a y^{4}$

(2)、解不等式组 ${\begin{array}{l} \frac{1}{2} (x + 3) < 2 \\ \frac{x + 2}{2} > \frac{x + 3}{3} \end{array}$

查看试题解析
20.

(1)、先化简，再求值： $(1 - \frac{3}{x + 2}) \div \frac{x^{2} - 2 x + 1}{x^{2} - 4}$ ，其中 $x = \frac{1}{2}$

(2)、解方程： $\frac{x}{2 x - 3} + \frac{5}{3 - 2 x} = 4$

查看试题解析
21. 如图，在平面直角坐标系中， $Δ A B C$ 的三个顶点都落在格点上（每个小方格都是边长为1各单位长度的正方形），点的坐标为.
（ 1 ）将 $Δ A B C$ 向左平移6个单位再向上平移2个单位长度，得到 $Δ A_{1} B_{1} C_{1}$ ，请画出 $Δ A_{1} B_{1} C_{1}$ ，并写出 $A_{1}$ 的坐标；

（ 2 ）画出 $Δ A B C$ 关于原点O成中心对称的 $Δ A_{2} B_{2} C_{2}$ ，并写出 A₂的坐标；

查看试题解析
22. 如图，在 $Δ A B C$ 中， $A B = A C$ ，点D，E，F分别在AB，BC，CA上，且 $B D = C E ， B E = C F$ .

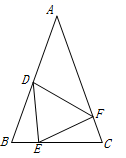(1)、求证： $Δ D E F$ 是等腰三角形；

(2)、当 $∠ A = 60^{°} ， D E = 6$ ，直接写出 $Δ D E F$ 的面积；

查看试题解析
23. 为了改善社区环境，某社区计划对3600平方米的区域进行绿化，社区委员会对甲乙两个工程队考查发现，甲队每天能完成的绿化面积是乙队每天能完成绿化面积的 $1.5$ 倍，如果两队各自独立完成社区的绿化任务，甲队比乙队少用10天，求甲乙两个工程队每天各能完成多少绿化面积.

查看试题解析
24. 如图，在四边形ABCD中， $A D / / B C ， ∠ A = ∠ C ， ∠ A B C$ 的平分线交CD于点E，

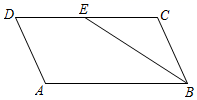(1)、求证：四边形ABCD是平行四边形；

(2)、当E是CD中点，AD=3时，求四边形ABCD的周长；

查看试题解析
25. 某单位要印刷一批宣传材料。在甲印刷厂不管一次印刷多少页，每页收费0.1元，在乙印刷厂，一次印刷页数不超过20时，每页收费0.12元，一次印刷页数超过20时，超过部分每页收费0.09元，设该单位需要印刷宣传材料的页数为x（x>20且x是整数），在甲印刷厂实际付费为 $y_{1}$ （元），在乙印刷厂实际收费为 $y_{2}$ （元）

(1)、分别写出 $y_{1}, y_{2}$ 与x的函数关系式；

(2)、你认为选择哪家印刷厂印刷这些宣传材料较好？为什么？

查看试题解析
26. 如图， $∠ A O B = 120 °$ ，OC是 $∠ A O B$ 的平分线，点E，M分别在射线OA，OC上，作射线ME，以M为中心，将射线ME逆时针旋转60度，交OB所在的直线于F，

(1)、按要求画图，并完成证明；过点M作MH//OA，交射线OB于H，求证： $Δ O M H$ 是等边三角形；

(2)、当点F落在射线OB上，请猜想线段OE，OF，OM三者之间的数量关系；

(3)、当点F落在射线OB反向延长线上，请猜想线段OE，OF，OM三者之间的数量关系；

(4)、点G是射线OA上一点，且满足OG=8，若MG=7，OF=1.5，请直接写出OE的长；

查看试题解析