山东省潍坊市青州市2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在 , , , 中,分式有( )A、1个 B、2个 C、3个 D、4个3. 要使分式 无意义,则 的取值范围是( )A、 B、 C、 D、4. 如图,用直尺和圆规作已知角的平分线,要证明 成立的全等三角形的判定依据是( )
2. 在 , , , 中,分式有( )A、1个 B、2个 C、3个 D、4个3. 要使分式 无意义,则 的取值范围是( )A、 B、 C、 D、4. 如图,用直尺和圆规作已知角的平分线,要证明 成立的全等三角形的判定依据是( ) A、 B、 C、 D、5. 如图, , ,若 ,则还需添加的一个条件有( )
A、 B、 C、 D、5. 如图, , ,若 ,则还需添加的一个条件有( )
 A、1种 B、2种 C、3种 D、4种6. 若点 与点 关于 轴对称,则 等于( )A、-3 B、-5 C、1 D、37. 已知等腰三角形的一边长为 ,另一边长为 ,则它周长是( )A、 B、 C、 D、 或8. 如图,在 中, 的平分线与 的垂直平分线交于点 ,连接 ,若 , ,则 的度数为( )
A、1种 B、2种 C、3种 D、4种6. 若点 与点 关于 轴对称,则 等于( )A、-3 B、-5 C、1 D、37. 已知等腰三角形的一边长为 ,另一边长为 ,则它周长是( )A、 B、 C、 D、 或8. 如图,在 中, 的平分线与 的垂直平分线交于点 ,连接 ,若 , ,则 的度数为( ) A、12° B、31° C、53° D、75°9. 如图,若△MNP≌△MEQ,则点Q应是图中的( )
A、12° B、31° C、53° D、75°9. 如图,若△MNP≌△MEQ,则点Q应是图中的( ) A、点A B、点B C、点C D、点D10. 如图,在△ABC中,AB=AC,BC=10,S△ABC=60,AD⊥BC于点D,EF垂直平分AB,交AB于点E,AC于点F,在EF上确定一点P,使PB+PD最小,则这个最小值为( )
A、点A B、点B C、点C D、点D10. 如图,在△ABC中,AB=AC,BC=10,S△ABC=60,AD⊥BC于点D,EF垂直平分AB,交AB于点E,AC于点F,在EF上确定一点P,使PB+PD最小,则这个最小值为( ) A、10 B、11 C、12 D、1311. 如图, 中, , ,将其折叠,使点 落在边 上 处,折痕为 ,则 等于( )
A、10 B、11 C、12 D、1311. 如图, 中, , ,将其折叠,使点 落在边 上 处,折痕为 ,则 等于( ) A、15° B、30° C、10° D、20°12. 对于非零实数 ,规定 ,若 ,则 的值为( )A、 B、 C、 D、
A、15° B、30° C、10° D、20°12. 对于非零实数 ,规定 ,若 ,则 的值为( )A、 B、 C、 D、二、填空题
-
13. 如图,在 中,点 为 的中点, ,若 , ,则 .
 14. 已知:如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB=度.
14. 已知:如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB=度.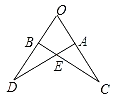 15. 已知 ,则 .16. 如图,点 在 内部,且到三边的距离相等,若 ,则 .
15. 已知 ,则 .16. 如图,点 在 内部,且到三边的距离相等,若 ,则 . 17. 关于x的方程 有增根,则k的值是.18. 已知 ,则 , .
17. 关于x的方程 有增根,则k的值是.18. 已知 ,则 , .三、解答题
-
19. 计算和化简求值.(1)、计算:(2)、计算:(3)、先化简再求值: ,其中 , .20. 解分式方程(1)、(2)、21. 如图,完成下列推理过程:
如图所示,点E在 外部,点D在BC边上,DE交AC于F , 若 , ,
求证: .

证明:∵ (已知),
( ▲ ),
∴ ( ▲ ),
又∵ ,
∴ ▲ ▲ ( ▲ ),
即 ,
在 和 中
(已证)
∵ (已知)
(已证)
∴ ( ▲ ).
∴ ( ▲ )
22. 某文化用品商店用 元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高 元,商店用了 元,所购数量是第一次的 倍.(1)、求第一批采购的书包的单价是多少元?(2)、若商店按售价为每个书包 元,销售完这两批书包,总共获利多少元?

